ASTR 222 — Galaxies & Cosmology

Homework 2 — Due 23 Feb in class

1. Galactic Rotation
   The Sun orbits the Galaxy at ~220 km/s at a distance of ~8 kpc from the center.
   1. Assuming that the Sun moves in a circular orbit, what is the period of the Sun’s orbit? Estimate how many revolutions of the Galaxy have occurred in its lifetime.
   2. Use Kepler’s third law to estimate the mass of the Galaxy (interior to the Sun).
2. Galactic Parallax
   

   Use half of the period of the Sun’s orbit determined in the previous problem to find the amount of time it would take to determine a “Galactic parallax”. What would be the number of parsecs in a “galsec”, the distance of a galaxy whose galactic parallax equals 1.0”? Is this a feasible or realistic way to determine distances to other galaxies? Explain your reasoning.

3. Galactic Luminosity
   

   Suppose the Milky Way consists of 2.7 x 10¹¹ stars identical to the Sun. What is the total luminosity and total absolute magnitude of the entire Galaxy? Given the approximate relative sizes of the major components (disk, bulge/bar, halo), what are the luminosity and absolute magnitudes of those components? Do these values make sense? Are each likely to be over or under estimated. Explain your reasoning.

4. Supermassive black hole
   
   

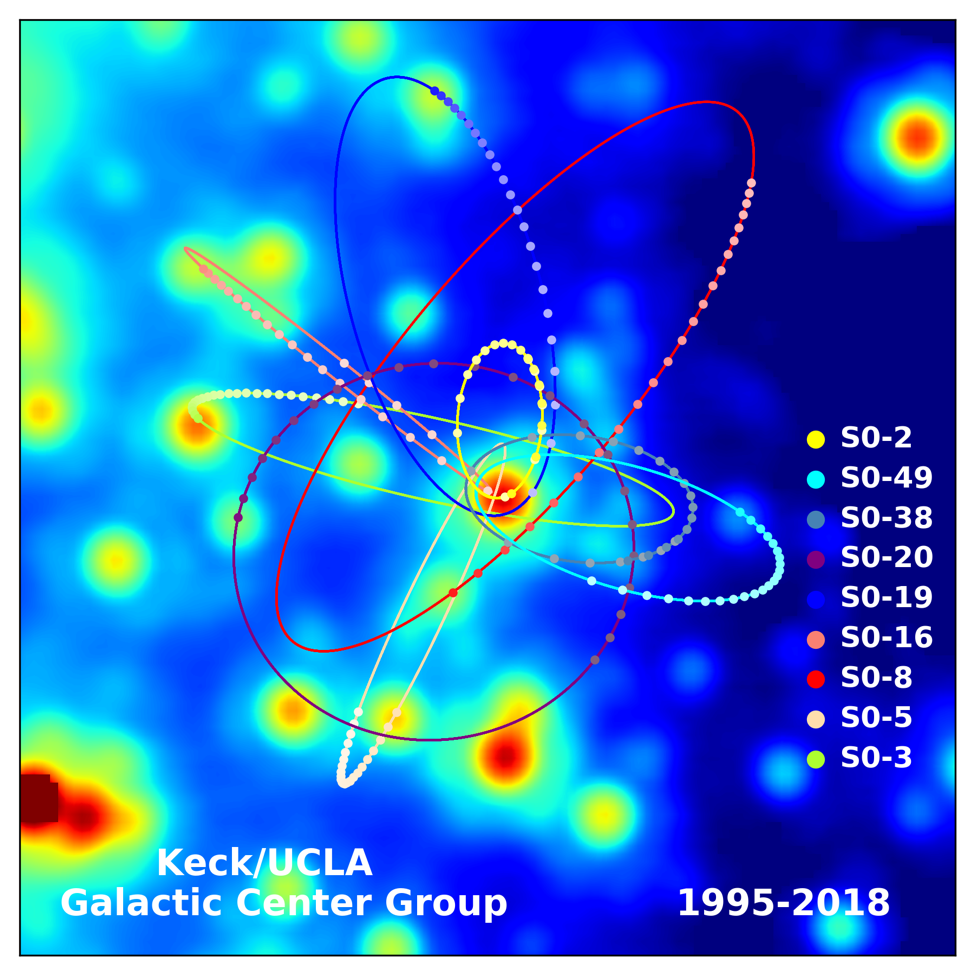
   The above image shows the orbits of stars around the supermassive black hole at the center of the Milky Way. This image is 1 arcsecond per side. Each of the colored lines in this image represents the orbit of a star around the central object. The dots on the line represent a step of 1 year, and are shaded according to the date of observation (whiter=older).

   1. Using the dots and the scale of the image, estimate the orbital period (in years) and semi-major axis (in AU) of the two stars with completed orbits, S0-2 and S0-38.
   2. Using these values, estimate (separately for each star) the mass of the central object in solar masses. Do the values agree? If not, why not? What is the published mass of the central supermassive black hole? Do the values you calculated agree with the published value? Why or why not?
5. Studying the Galaxy with Globular Clusters
   Here is a list of (real!) data for globular clusters. This is the same data you used in HW1, so feel free to reuse code from there to get started!

   We can use the observed velocities of the globular clusters to get the rotation speed of the Galaxy.

   • Plot Vr (on the y-axis) against l (on the x-axis). Only use the metal-poor globular clusters for this exercise. Why? You should see a lot of dispersion, but a hint of a sinusoidal trend. At l=90 the radial velocities are more negative, at l=270 they are more positive. This is because the globular cluster system isn’t rotating. Remember that l=90 points along the direction of rotation; clusters along l=90 are in front of us and we are moving towards them, so they have a negative (approaching) radial velocity (and vice versa for the clusters at l=270). Note: Make sure not to include clusters which have no measured Vr in your analysis!

   So we should be able to fit a sine function to the data: Vr = -Vc,proj sin(l). Once you have solved for Vc,proj, remember we have to deproject this value to get the true rotation speed. Since Vc,proj = Vc<cos(b)>, averaging over all b’s, we have Vc,proj = (2/π)Vc. So to correct for projection, Vc = (π/2)Vc,proj.

   • Fit this sine curve to the data, and derive Vc, the circular velocity of the Milky Way. How does your value compare to the “standard” value of 220 km/s?

   Coding alert: remember you dont actually have to do a sine fit of Vr versus l which would be a complicated non-linear fit. Instead, fit Vr versus sin(l), which is a simple linear fit! (But remember to convert l to radians when using the sine function!)