ASTR 222 — Galaxies & Cosmology

Homework 4 — Due 25 April in class

1. Galactic collisions

   1. The mass density of stars in the solar neighborhood is approximately 0.05 Msun per cubic parsec. Assuming mass density is constant and that all of the stars are main-sequence M stars, estimate the fraction of the Galactic disk's volume that is occupied by stars.
   2. Suppose that an intruder star (a main sequence M star) travels perpendicularly through the Galactic disk. What are the odds of the intruder colliding with another star during its passage through the disk? Take the thickness of the disk to be approximately 1 kpc. If an identical galaxy collided with the Milky Way perfectly face on, what are the odds of ANY star colliding with ANY OTHER star?

2. The age of a flat, matter-only universe

   Start with the Friedman equation:

   

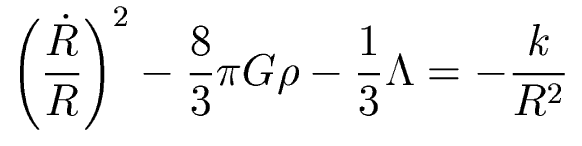
   Integrate the Friedman equation for a flat, matter-only universe (ie no cosmological constant), to show that the age of the universe in this model is t₀=(2/3)(1/H₀). Describe simplifying assumptions, and show your work step by step.

3. Early and Late Cosmological Expansion

   Start again with the Friedman equation, and assume that we have a universe that is spatially flat. In the following two situations, explain which terms on the Friedman equation are important and which you can ignore or set to zero. Then integrate the Friedman equation to solve for how the scale factor of the universe changes with time – in other words, solve for R(t).

   1. In the early universe, the energy density of radiation exceeded that of matter, and at this point in time (referred to as the “radiation era”) radiation drove the expansion. Solve for R(t) under these conditions.

   2. Now consider very late times in a universe with a non-zero cosmological constant. Again solve for R(t) under these conditions.