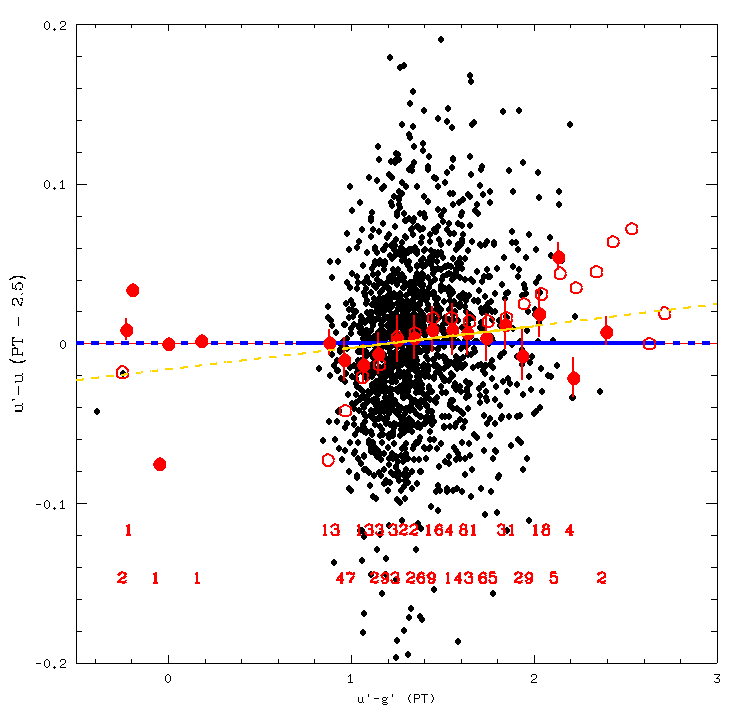
Below is the transform from u'-g' to u'-u using Zeljko's data. I decided that the linear fit (the gold line) was the best fit for this transform,
and so the transform equation is u'-u = .013599889*(u'-g') -.016431401. The dashed line shows the whole curve, while the solid line
indicates the region I think the curve is valid for, in this case between u'-g' of .95 and 2.
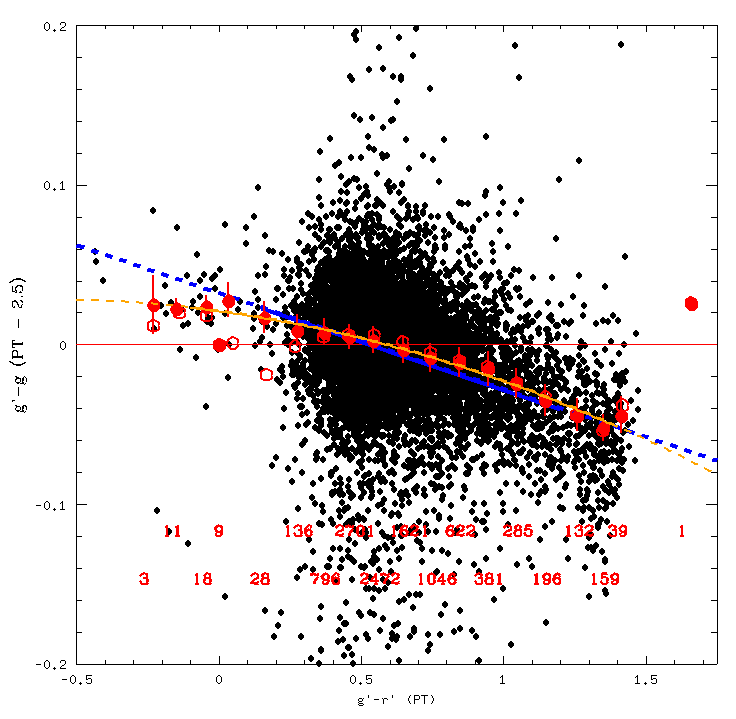
Below is the transform for g'-r' Vs g'-g. A quadratic fit of the form g'-g = -.020198157*(g'-r')^2 -.023396039*(g'-r') + .02074906 works
nicely, and is shown in orange on the plot. The fit is good for g'-r' between -.1 and 1.4.
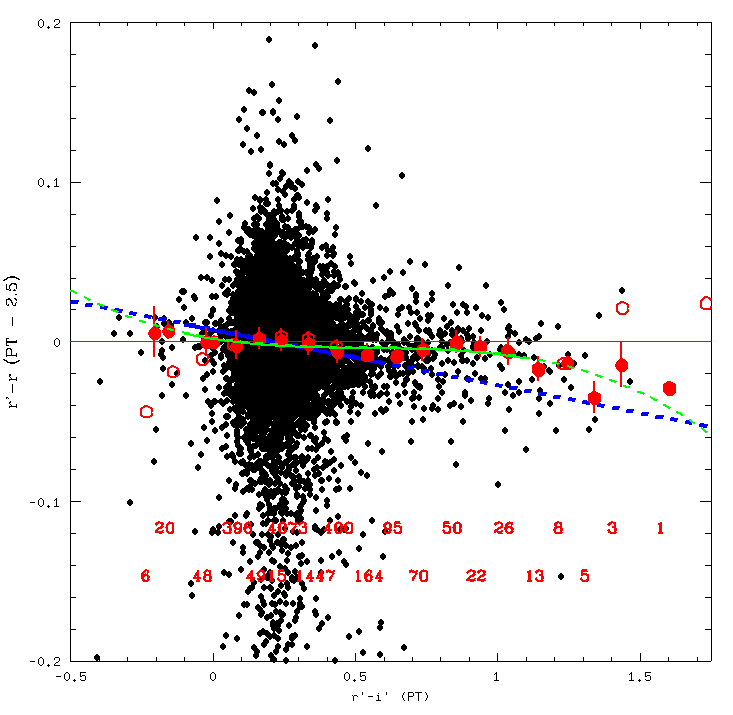
Next up is r'-i' Vs r'-r. A cubic fit (in green) seems to work best here, and it is described by the equation r'-r = -.029779941*(r'-i')^3 + .048483334*(r'-i')^2 -.028378565*(r'-i') -.0017277173.
I judged this fit to be good between r'-i' of -.1 and 1.1.
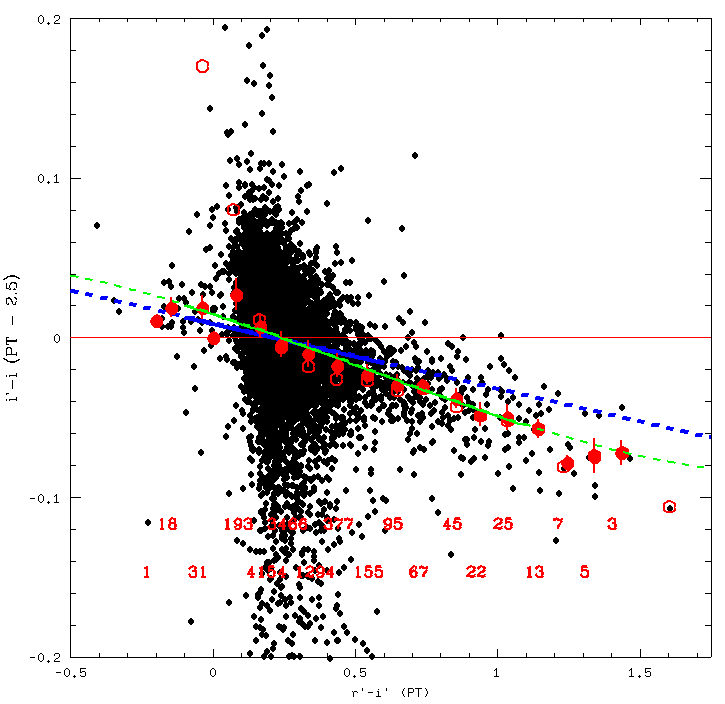
The cubic fit(green again) also fits well for r'-i' Vs i'-i. Its equation is i'-i = .0097545022*(r'-i')^3 -.015713306*(r'-i')^2 -.057863005*(r'-i') + .014577996. Again, the fit is good
between r'- i' = -.1 and 1.1.
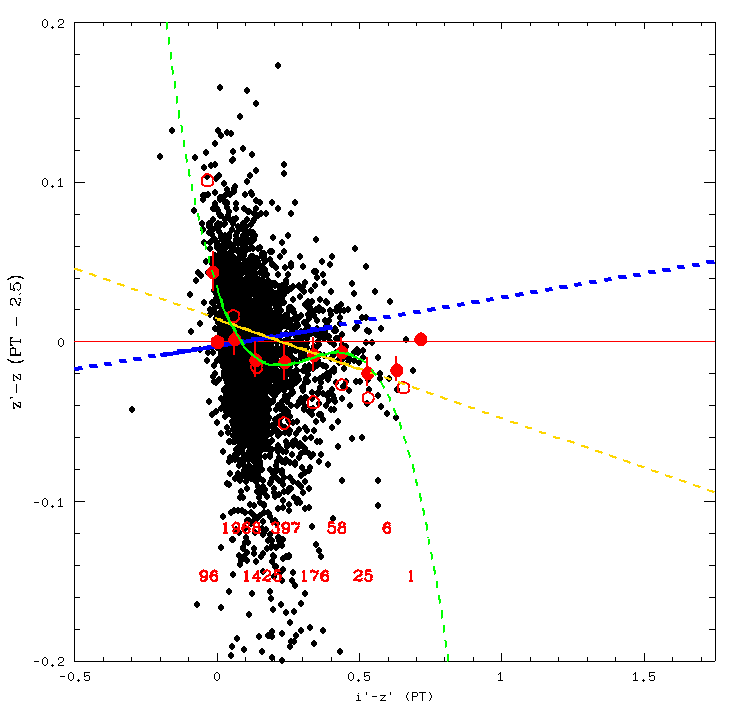
Last up is the i'-z' Vs z'-z transform, which is just a mess. Im going with the linear fit on this one, just because i think
the dramatic curving nature of the quadratic and cubic are gonna mess us up more than the fact that the linear fit just isn't a great fit.
I'm gonna give both the cubic and the linear fit though, just for good measure. The cubic (green): z'-z = -1.876117*(i'-z')^3 + 1.809729*(i'-z')^2 -.5221147*(i'-z') + .032153267.
The linear (gold): z'-z = -.062326316*(i'-z') + .013975264. The fits work when 0 < i'-z' < .5.