Solutions for Homework #4
Astronomy 100, Fall 2002
Chapter 4, Review 2
What is the difference between an isotope and an ion?
To answer this question, we need to know what an isotope is and what an ion is, so this is a question about atomic structure. In an atom there are three basic types of particles: protons (one positive charge each), neutrons (no charge), and electrons (one negative charge each). The electrons orbit the nucleus, a cluster of protons and neutrons. Changing the number of protons in the nucleus changes what element you have, so what does changing the number of neutrons or electrons do? Letís address electrons first. Their negative charge serves to balance out the positive charge of the protons in the nucleus, so if you have a neutral atom (one that has no net charge) then the number of electrons in the atom is equal to the number of protons. If you change the number of electrons, you change the net charge (more electrons than protons gives a negative charge; fewer electrons than protons results in a positive charge). If an atom has a net charge, it is called an ion. So, we can conclude that an ion means an atom with the same number of protons, but a different number of electrons. This doesnít change what element it is, just what charge it carries. Similarly, changing the number of neutrons wonít change what element you have, so we call this an isotope. Note that since neutrons donít have charge, changing the number of neutrons doesnít change the net charge of the atom. You have to detect different isotopes by comparing their atomic masses. Anyway, to summarize, an isotope refers to the number of neutrons in an atom; an ion refers to the number of electrons.
For more information related to this problem, see pp. 89-90 in your book.
Chapter 4, Problem 1
Human body temperature is about 310 K (98.6° F). At what wavelength do humans radiate the most energy? What kind of radiation do we emit?
Because humans are made mostly out of really dense matter (water, bones, etc.), we can approximate the radiation spectrum of a person with a blackbody spectrum. This means that we can use Wienís Law (see By The Numbers 4-1 on p. 95 of your book) to calculate the maximum wavelength of radiation for a human. Wienís Law says that
![]()
This formula is written so that if you put T in Kelvin, you get back the max wavelength in nanometers (1 nm = 10-9 m). Fortunately they gave us T in Kelvin already, so we can just plug it in:
![]()
Looking on a diagram of the electromagnetic spectrum (like the one on p. 66 of your book, in Figure 3-2), we see that this wavelength corresponds to infrared radiation, also known as body heat!
Chapter 10, Review 13
Why does nuclear fusion in the Sun occur only near the center?
To answer this question letís examine the conditions needed for nuclear fusion to occur. First of all, to start fusion, the material needs to be very hot. Think about the definition of temperature as the speed with which atoms and molecules in a material are moving around. The hotter the gas, the faster the molecules are going. This is important because to overcome the force repelling two positive hydrogen nuclei (really just two protons) so they can fuse, they need to hit each other at huge speeds. You know about the force they have to overcome if youíve ever tried to force two strong magnets together with like poles facing each other Ė itís the same idea with these protons (although itís not the same force, it varies similarly). Anyway, they have to be really going fast in order that they can get close enough together that an even stronger, attractive force (known creatively as the "strong force") pulls them together and they fuse into a helium nucleus. This only works at really short range, so that any temperature below about 10 million Kelvin means that the protons donít have enough speed to get this close and fuse. Thatís the first condition.
The second condition is that the material has to be very dense. By making the material denser, you increase the probability that the protons will run into each other at all. Anything less than really dense, and the rate of fusion wonít be very high at all: remember these protons are tiny Ė 1.6 x 10-15 meters in diameter (see the Critical Inquiry on p. 91 for an idea of how small this is). So you need something really dense, with lots and lots of nuclei around, before you get enough of them running into each other to get a reasonable rate of fusion.
So where in the Sun do these two conditions meet up? As you get closer and closer to the center of the Sun, the amount of stuff pressing inward (due to gravity, which wants to make everything collapse into a point at the center) gets larger and larger, so the pressure (and therefore the density) goes up. The temperature goes up as well - based on what we know about gases, pressure and temperature are proportional to one another. In fact, the temperature at the very center of our Sun is only around 15 million Kelvin, so only right at the center is it hot enough and dense enough for fusion to occur.
Chapter 11, Review 5
Why does the luminosity of a star depend on both its radius and its temperature?
This question is best addressed by examining the formula found in By the Numbers 11-3 on p. 258 of your book:
![]()
This formula is also known as the Stefan-Boltzmann Law. Each pair of parentheses encloses a meaningful unit of this formula. The first one is the surface area of the star; the second is the energy per unit area per unit time emitted by a blackbody. Also remember that the word "luminosity" refers to the total energy output of the star, per unit time. So first, if we say (with good reason) that a star emits blackbody radiation (as discussed back in chapter 4), then we can say that the energy it emits per unit area, per unit time, is sT4. s ("sigma") is a constant that varies depending on what units T and the energy are given in. Thatís where the temperature dependence comes from. Then we want to multiply this by the total area that is emitting that energy per unit time Ė the surface area of the star, which we assume is a sphere, so we can write the surface area as 4pR2. Thatís where the radius dependence comes from. Another way to think about this is:
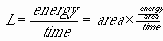
Chapter 11, Problem 9
Find the luminosity and spectral type of a 5-M¤ main-sequence star.
Since this star is on the main sequence, we can use the mass-luminosity relation given in By the Numbers 11-5 on p. 271 of your book to calculate the luminosity:
![]()
as long as the mass and luminosity are given in terms of the solar mass and luminosity. In other words, if you plug in a mass as a number of solar masses, you get out a luminosity as a number of solar luminosities. In this case, our star has 5 times the solar mass, so plug in M=5:
![]()
So our star has 280 times the luminosity of the Sun! Once we know this, we can use the Hertzsprung-Russell Diagram to get its spectral class, since the diagram arranges stars by their spectral class (or temperature) and luminosity (or magnitude). In this case we want to find what the spectral class is of stars on the main sequence with 280 times the luminosity of the Sun. Figure 11-10 on p. 259 in the book is an H-R diagram; it shows that main-sequence stars between about 100 and 10,000 times the luminosity of the Sun are classified as B stars, so this star, with L = 280 L¤ , is of spectral class B.