Homework 4, due April 6, 2004

Chapter 4, problem 13 (5 points): The labeled transitions below represent an electron moving between energy levels in hydrogen. Answer each of the following questions and explain your answers.

a) Which transition could represent an electron that gains 10.2 eV of energy?

Transition B – the electron absorbs a photon and is able to jump to a level with higher energy, the energy difference between the levels is 10.2 eV

b) Which transition represents an electron that loses 10.2 eV of energy?

Transition C – the electron jumps from the 10.2 eV level down to the 0.0 eV level and has to get rid of the extra energy – it sends off a photon with an energy equal to the difference of 10.2 eV

c) Which transition represents an electron that is breaking free of the atom?

Transition E – the electron gains so much energy that it can leave the atom, left is a free electron and an ionized atom

d) Which transition, as shown, is not possible?

Transition D – You cannot have an electron in between the discrete orbits.

e) Describe the process taking place in transition A.

The electron can jump more than one level at a time, as long as energy is conserved. In this case, it has to send off a photon with 12.1 eV to be able to go directly to the ground state.

Chapter 6, problem 11 (5 points): Suppose the surface temperature of the Sun were about 12,000 K, rather than 6,000 K.

a) How much more thermal radiation would the Sun emit?

Stefan-Boltzman law: L ~ R²T⁴ ® L₂ ~ R²T₂⁴ = R²*(2*T₁)⁴ = 2⁴*R²T⁴ = 16*L₁

® it would emit 16 times more thermal radiation

b) How would the thermal radiation spectrum of the Sun be different?

Wien’s law: l_peak ~ 1/T ® a hotter star has a lower peak wavelength and is brighter ® spectrum would be shifted towards the blue

® l_peak = 2,900,000/12,000 = 242 nm which is in the UV

c) Do you think it would still be possible to have life on Earth? Explain.

Life would probably still be possible, but more difficult. The increase in UV radiation would affect our atmosphere. The Earth will get hotter as well, since the Sun would put out more total radiation.

Chapter 12, problem 9 (5 points): The total mass of the Sun is about 2x10³⁰ kg, of which about 75% was hydrogen when the Sun formed. However, only about 13% of this hydrogen ever becomes available for fusion in the core; the rest remains in layers of the Sun where the temperature is too low for fusion.

a) Based on the given information, calculate the total mass of hydrogen available for fusion over the lifetime of the Sun.

b) The only hydrogen available are the 13% of the total amount of hydrogen which is in the core. The total amount of hydrogen is 75% of the total mass.

® 13% of 75% of 2x10³⁰ kg = 0.13 * 0.75 * 2x10³⁰ kg = 1.95x10²⁹ kg

c) Combine your results from part (a) and the fact that the Sun fuses about 600 billion kg of hydrogen each second to calculate how long the Sun’s initial supply of hydrogen can last. Give your answer in both seconds and years.

600 billion kg = 1.95x10²⁹ kg ® x = 1.95x10²⁹ kg * 1sec = 3.25x10¹⁷ seconds

1 sec x 600x10⁹ kg

1 year = 31,536,000 sec ® x = 1.03x10¹⁰ years = 10.3 billion years

The Sun can burn hydrogen for 10 billion years.

c) Given that our solar system is now about 4.6 billion years old, when will we need to worry about the Sun running out of hydrogen for fusion?

10.3 billion – 4.6 billion = 5.7 billion years ® We should start worrying about that in about 5.4 billion years, if we are still here than.

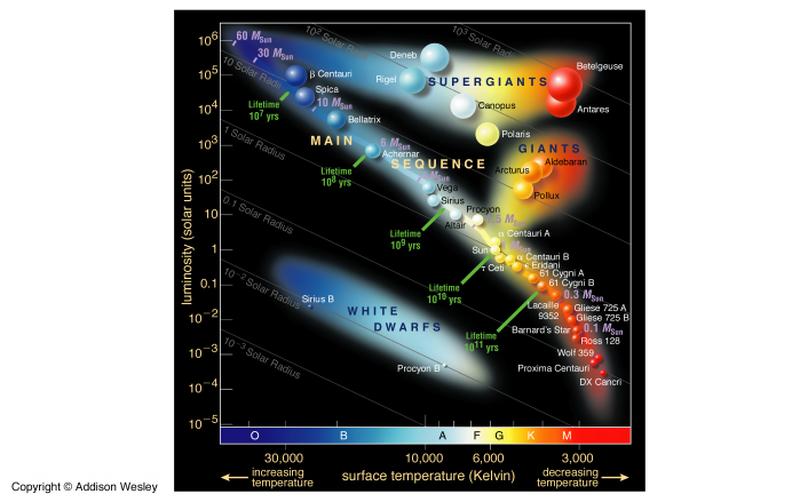
Chapter 13, problem 12 (5 points): Draw a sketch of a basic Hertzsprung-Russel diagram (H-R diagram). Label the main sequence, giants, supergiants, and white dwarfs. Where on this diagram do we find stars that are cool and dim? Cool and luminous? Hot and dim? Hot and bright?

Cool and dim: lower right corner (low temperature, low luminosity)

Cool and luminous: upper right corner (low temperature, high luminosity)

Hot and dim: lower left corner (high temperature, low luminosity)

Hot and bright: upper left corner (high temperature, high luminosity)