Astronomy 100
Homework #2 Solutions
Due date: 2/24/04
Chapter 3, p. 83, Review #13
State Kepler’s three laws of motion, and
explain the meaning of each.
I.
“… the orbit of each
planet about the Sun is an ellipse with the Sun at one focus.”
II.
“… as a planet moves
around its orbit, it sweeps out equal areas in equal times.”
III.
P2 = a3,
where “P” is the orbital period in years, and “a” is the semi-major axis
(average distance from the Sun) in Astronomical Units (A.U.s)
(p. 77)
Law I means that the planets
do not orbit in perfect circles with the Sun at the center, as previously
thought (which required epicycles!).
Rather, their orbits are elliptical, and the Sun is at one focus. There is nothing at the other focus.
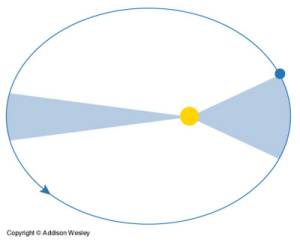
Law II simply means that
planets move faster as they approach the Sun, and more slowly when they are
further away. The blue shaded regions
in the diagram below have equal area.
Hence, one can see that if this occurs in the same amount of time, the
planet must travel a greater distance when it is closer to the Sun, and
therefore must be moving faster.
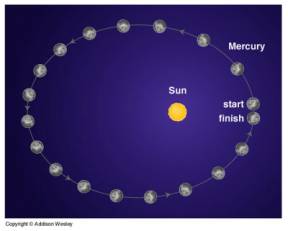
An outer planet, such as
Jupiter, is always farther away from the Sun than an inferior planet like
Mercury. Hence, it should always be
moving more slowly. Law III relates a planet’s
average distance from the Sun with its period.
Basically, the closer a planet is to the Sun, the faster it will
complete one entire orbit. The third
law allows us to calculate values precisely.
Chapter 4, p. 95, Review #2
What is the formula for kinetic energy of
an object? Based on this formula,
explain why (a) a 4-ton truck moving at 100 km/hr has 4 times as much kinetic
energy as a 1-ton car moving at 100 km/hr; (b) a 1-ton car moving at 100 km/hr
has the same kinetic energy as a
4-ton truck moving at 50 km/hr.
Kinetic energy is an “energy
of motion” and must depend on an object and its motion, or velocity.
Kinetic
Energy = (1/2) m * v2
m -> the
mass of the object
v -> the object’s velocity
If “m” is measured in
kilograms, and “v” in km/s, the energy will be in units of Joules.
(p.
86)
(a) Since kinetic energy is linearly proportional to mass,
for two objects traveling at the same speed, the ratio of their kinetic
energies will simply be equal to the ratio of their masses. (Since we are comparing two objects measured
in tons instead of kg, these units will cancel out. So, don’t worry about it!
To get your answer in Joules, you would have needed to convert tons to
kilograms.)
(1/2)(4
tons)(100 km/hr)2 = 20,000 units
(1/2)(1
ton)(100 km/hr)2 = 5,000
units
5,000 x 4 = 20,000
ü 4 times the kinetic energy!
(b) If objects have different masses, but exactly the
right velocities, it is possible for them to have the same kinetic energy. Precisely, if the velocity is half as fast,
the mass must be four times as great.
This occurs because of the v2 term.
?
(1/2)(1
ton)(100 km/hr)2 = (1/2)(4 ton)(50 km/hr)2
(1/2)(10,000) (2)(2,500)
5,000 = 5,000 ü Equivalent!
Chapter 4, p. 95, Review #6
What is the law of conservation of energy?
Your body is using it right now to keep you alive. Where does this energy come from? Where does it go?
The law of conservation of
energy states that although energy may change forms, the total amount of energy
never changes. The “fuel” to keep a
human body’s “engine” running comes directly from food. If you ate a bagel for breakfast this
morning, this is providing the energy for you to function right now. Food has a certain amount of stored
potential energy that is utilized once the body digests it. However, if you are considering first
principles, the stored energy in food comes from the Sun. And you could even think of where the Sun
gets it energy… (
p. 89)
The energy that was stored in
the bagel you ate for breakfast, has now changed forms. The energy goes to a variety of
functions. For example, your body uses energy
to keep itself at a consistent temperature, allows your muscles to do work,
etc. For anyone who has taken a biology
course, you should remember that this is quite a complicated process!
Chapter 5, p. 108, Review #7
Why does a spaceship require a high speed
to achieve orbit? What would happen if
it were launched with a speed greater than the Earth’s escape velocity?
In order to achieve orbit,
any object must be moving fast enough so that the centripetal force outward
balances the large force of gravity, pulling the object towards the Earth. Since the Earth is a very large and massive
object relative to a spaceship, high speeds are required. In the diagram below, the first two arrows
represent an object moving too slowly.
In these cases, gravity wins, and the object eventually falls to the
surface of the Earth. The third arrow
represents an object traveling at a high enough speed to achieve orbit.
Fcentripetal = (mv2)
/ r
Fgravity = (GMm) / r2
In orbit, these forces are
balanced, so (mv2) / r = (GMm) / r2. And, the velocity necessary will depend on
the height of the orbit: v2
= (GM/r).
Escape velocity is the speed
in which the centripetal force outward exceeds the force of gravity
inwards. If objects move faster than
escape velocity, they will be launched from the Earth, and will head out into
the Solar System. This is represented
by the fourth arrow in the diagram below.
[i.e., if v2 > (GM/r)]
