- a) Write the Friedmann equation in terms of Ωs and the redshift z
and its time derivative. Ignore the curvature and cosmological constant terms
to obtain an expression for t(z), the age of the universe at redshift z.
[Hint: dz/dt plays a key role in this derivation. Keep Ωm0 as a variable: do not set it to unity even though we're ignoring curvature.] - b) How good is this approximation?
Solve the full Friedmann equation numerically
and plot t(z) for the full numerical solution along with the expression from
(a) out to z = 5.
Assume H0 = 70 km/s/Mpc,
Ωm0 = 0.3, and
ΩΛ0 = 0.7.
[Hint: you can write your own code if you like; astropy has a cosmology package that does most of the work required. One may also use on-line cosmology calculators. - c) It is fairly straightforward to age-date young stellar populations.
Suppose a galaxy observed at z = 3 has spectral characteristics that indicate it has an age of 2 Gyr. What age does this imply for the universe now?
In the local universe, we often use Hubble's Law (V = H0Dp) to get distances to galaxies using their observed recession velocity. But we've seen that distances take on different definitions on cosmological scales. So how far out in redshift we can go using Hubble's Law before the errors introduced by ignoring cosmological effects become substantial? Let's imagine observing a Milky Way-like galaxy with an absolute magnitude of MV = -21 and a size of Rg = 20 kpc in a vanilla LCDM cosmology with H0 = 70 km/s/Mpc, Ωm0 = 0.3, and ΩΛ0 = 0.7.
Make plots of the following quantities as a function of redshift [log(1+z) from z = 0.01 to 1.0 works well] in two cases: (i) using Hubble's Law and (ii) using the correct cosmological quantity:
- a) The apparent magnitude of the galaxy. At what redshift does using Hubble's law introduce a magnitude error of 0.1 magnitudes? At what redshift is the magnitude wrong by 0.5 magnitudes?
- b) The apparent size of the galaxy [log(apparent size), in arcsec)]. At what redshift does Hubble's law introduce a size error of 10%? At what redshift does Hubble's law introduce a size error of 50%?
- c) The mean surface brightness of the galaxy. At what redshift have cosmological effects dimmed the surface brightness by 0.5 mag/arcsec^2?
Put the results for each part on the same graph so you can see the difference.
You'll end up with 3 plots (for a, b, and c), each with two lines.
Note that 0.1 magnitudes is a large error for modern photometry
(differences of < 0.01 mag. can be measured with care), so these
effects are readily discernable.
Professor Fink returns excited from an observing run because he has discovered a nova in a galaxy in the Virgo cluster, a key step in the distance scale. He knows that novae can be used as standard candles since they obey a luminosity--fade-time relation
MVpeak = -10.7 + 2.3 log(t2)
where t2 is the time in days that it takes for a nova to fade 2 magnitudes from its peak. (That's a base ten logarithm, as is conventional in astronomy.) Professor Fink hands you the data in the graph, and asks you to determine The Answer.
- a) What is the fade time t2? (Eyeball it.)
- b) What is the distance to Virgo from this?
- c) Supposing that Virgo has a recession velocity of 1400 km/s, what is H0?
- d) Fink assumes there is no extinction. How does the distance change if there is a little extinction, AV = 0.3? How does H0 change?
- e) Assume for the moment that AV = 0. What is the uncertainty in the distance determination?
- f) Not all novae are the same; there is some intrinsic dispersion in the luminosity--fade-time relation, about 0.5 mag. Galactic extinction maps suggest that the extinction is AV = 0.3 +/- 0.02. What now is the distance and its uncertainty? and H0?
(Keep in mind that the modern goal is to measure H0 to better than 2%.)
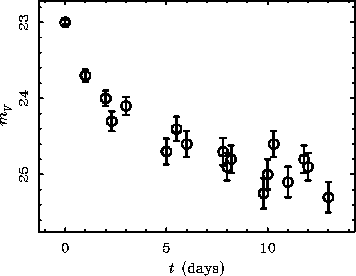
Light curve of nova in the Virgo cluster.
- a) Use Figure 1 from Metcalfe et al 1996 to estimate the logarithmic slope (dlogN/dm) of the galaxy number count function over the magnitude range
mB=21-26 for the following:
- the observed number counts;
- no evolution models;
- evolution models for q0=0.5 and q0=0.05.
- b) Using this dataset of magnitudes from the Hubble Ultra Deep Field create your own version of the Metcalfe plot, and calculate the slope of the observed galaxy number count function over that same magnitude range. The UDF covers 9 square arcminutes of sky. Make sure to cut out stars (objects with "stellarity" > 0.8 or so. What other quality control constraints might you wish to impose?)
- c) Discuss the comparison of your plot with that of Metcalfe etal, in the following terms:
- overall match in the curve
- match of the slopes
- evidence for galaxy evolution
ASTR/PHYS 428 only
- Plot the logarithm of the signal-to-noise as a function of magnitude. Include stars (high stellarity) as a different color or symbol type. Interpret what you see. Be sure to discuss the difference between stars and galaxies, any change in behavior at a particular magnitude, and any other noteworthy features.
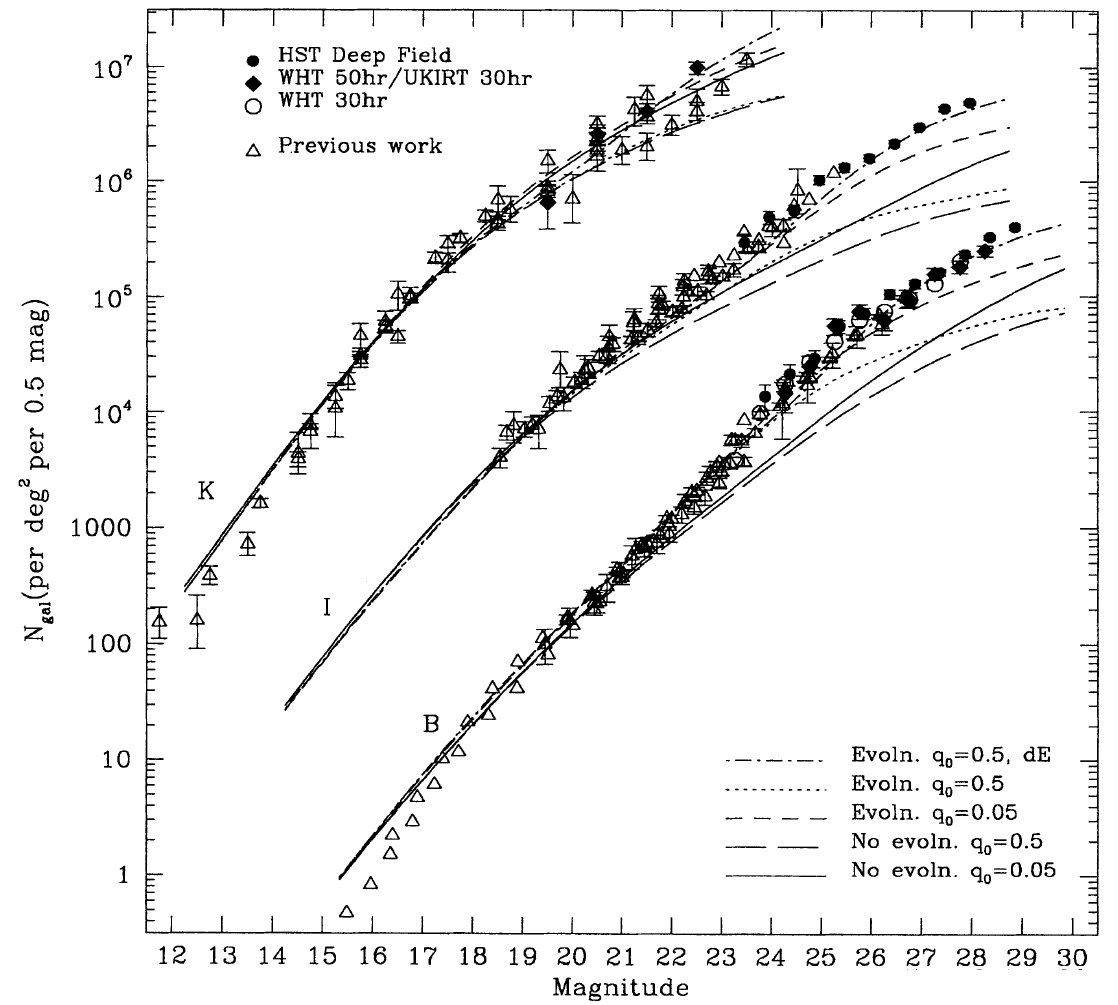
Galaxy number counts.
A portion of the Hubble Ultra Deep Field.
