Abell 520

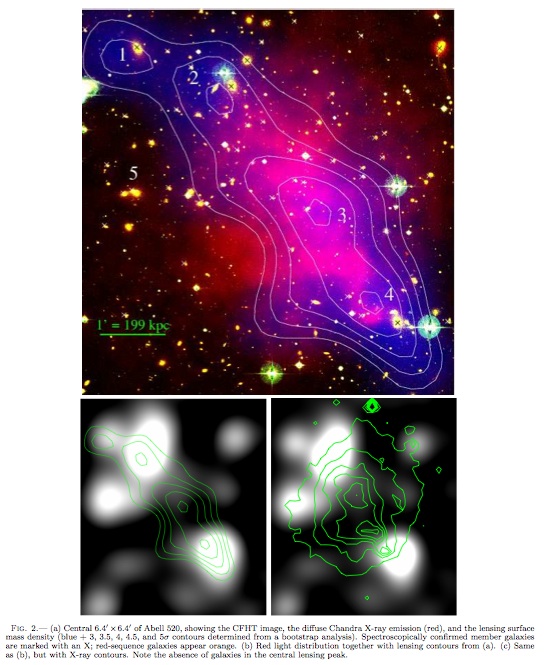
The galaxy cluster Abell 520 (image from Mahdavi et al.) shows a train wreck reminiscent of the bullet cluster. In this case however, the main mass peak coincides with the gas rather than the galaxies, opposite the situation in the bullet cluster.

The argument in the case of the bullet cluster is that most of the known baryons are in the gas, so you'd expect the mass traced by gravitational lensing to coincide with the gas. If we apply the same reasoning here, we would come to the conclusion that this case is consistent with modified gravity, opposite the situation for the bullet cluster. By the same token, the coincidence of the mass with the gas shouldn't happen in CDM: the dark matter should behave collisionlessly, and follow the galaxies. Though true in the bullet, that is not the case here.

Clearly, these are complicated systems. They are weird in any world view. I fear we run the risk of misleading ourselves if we draw sweeping conclusions from either of these systems, especially if we only focus on the one case that happens to agree with our preconceptions.

Personally, I find the residual mass discrepancy that all galaxy clusters suffer in MOND* much more challenging to the theory than any one case. Nonetheless, if this problem has some mundane solution in MOND (e.g., yet more baryons and/or heavy neutrinos) then we expect to see train wreck clusters like the bullet and Abell 520 fairly frequently. They should probably be relatively more common in MOND than in CDM. Moreover, their collision velocities should be systematically higher in MOND than in CDM because of the enhanced long range force in MOND. This effect actually gives a more natural explanation for the observed shock velocity (4700 km/s) in the bullet than can be obtained in CDM, where the maximum infall velocity obtained by gravitational attraction is 3800 km/s. The remainder has to be attributed to hydrodynamical effects and [predominantly] the rearrangement of the mass distribution and consequent deepening of the gravitational potential during the collision (see Springel & Farrar 2007, MNRAS, 380, 911 and Milosavljevic et al. 2007, ApJ, 661, L131).

* See the many papers by Sanders and others on the subject, going back at least to The & White (1988). This problem was also reviewed by Sanders and myself in ARA&A (2002) 40, 263. Note that we were highlighting this problem long before any NASA press release on the bullet.

Return to MOND home page