2005 BOOMERanG Data

July 2005: the BOOMERanG experiment reports new data extending to the third peak. This is ideally what we want: the same experiment measuring the first three peaks simultaneously.

The BOOMERanG peak ratio estimates (Jones et al. 2005) are shown together with the WMAP data here:

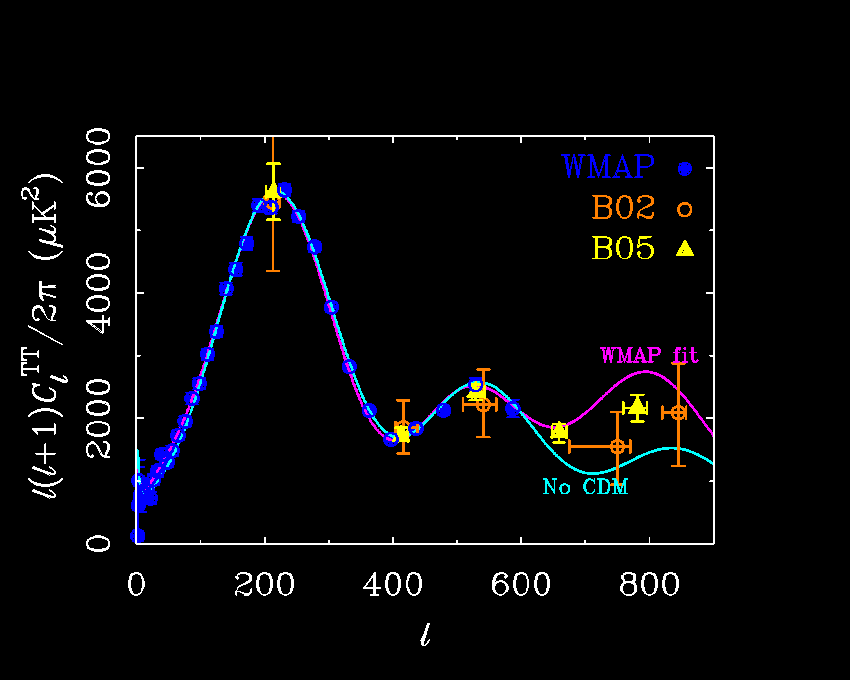CMB power spectrum as measured by WMAP (e.g., Spergel et al. 2003) and the peak locations measured by BOOMERanG (de Bernardis et al. 2002 [B02]; Jones et al. 2005 [B05]). The lines are the LCDM fit (pink) to the WMAP data and the no-CDM model of McGaugh (2004) (light blue).

The pink line is essentially the prediction of LCDM based on the WMAP data. The light blue line is the prior expectation for pure baryonic damping in the absence of cold dark matter. Strictly speaking, this has nothing to do with MOND; it is just the simplest expectation value for the shape of the power spectrum in a universe devoid of CDM.

The two lines are indistinguishable through the first two peaks. For LCDM, this is a fit. For no-CDM, it was an a priori prediction. This is an important distinction, since the a priori expectation of LCDM was a significantly larger second peak. In order to make this fit, one must adjust the baryon density, which is subject to checks against big bang nucleosynthesis, as discussed further below. Though both curves fit the WMAP first year data, they predict very different third peaks.

The BOOMERanG estimate for the third peak splits the difference. It is clearly higher than the prediction of the no-CDM model, so certainly does not falsify the existence of non-baryonic cold dark matter. A tolerable fit can be found with LCDM, but the fact that the third peak is a little lower than the second rather than a little higher may drive the need for a lot of tilt (MacTavish et al. 2005 report n = 0.86) and may revive talk of a running or broken power spectrum.

At present I would say LCDM "wins ugly" (to borrow a phrase from Ned Wright). This is not nominally what one would predict for the third peak (any more than for the second, which itself causes a conflict with BBN Lithium and Helium abundances - see McGaugh 2004). But LCDM has enough free parameters to fit the observed third peak; no-CDM does not. It remains to be seen whether TeVeS-type theories (Bekenstein 2004; Sanders 2005) might provide such freedom (e.g. Skordis et al. 2005). If so, MOND would "tie ugly," hardly a satisfactory situation.

Constraints from Big Bang Nucleosynthesis

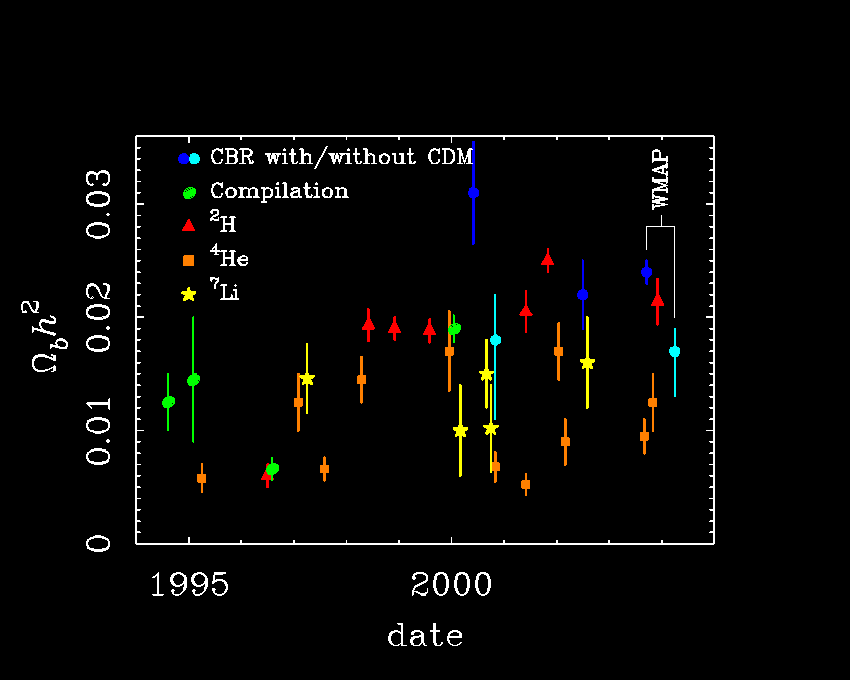Compilation of BBN constraints from (McGaugh 2004). The best fit to the CMB with CDM implies a very high baryon density, Obh2 = 0.024. This is necessitated by the low amplitude of the second peak, which is bang on the a priori no-CDM prediction. The latter was based on BBN (as of 1999) for which all data suggested Obh2 < 0.020. (The median of the data is Obh2 = 0.014.) The WMAP data are more consistent with the bulk of the data without CDM than with it.

Having done the exercise of reviewing all these data, I came away with greater respect for the Lithium determinations and less for Deuterium (which are certainly good, but over-hyped relative to the other nuclides). There are lots and lots of stars with measured Li, and the Spite plateau is remarkably well defined. Deuterium, as of this writing, is still based on only 5 objects, and the one done by an independent group has a clearly discrepant value (I refer to the one very high value, not the old low/high controversy). There is some hint of a systematic with column density, so I don't think it wise to trust these data to the exclusion of all else. I also worry about the trend for BBN estimates to grow since the advent of CMB data - it went from zero cases > 0.020 before BOOMERanG to that being the standard value afterwards. Does no one remember how H0 used to track the favored value with time? The uncertainties on the Helium abundance are clearly underestimated in many cases, but I found it very hard to push these data so far as to be happy with Obh2 > 0.020.

I begin to lose my enthusiasm for the ability of CMB data to tell us anything fundamental. Rotation curves already give a compelling test which - to my lasting surprise - MOND clearly wins. Most practicing cosmologists simply dismiss this, if they are even aware of it. I use to be the same way, until MOND reared its ugly head in my own data (for LSB galaxies). IF MOND is right, it won't be recognized until cosmological data become good enough for the cosmological community to unambigously share this experience. Clearly we're not there yet. IF, on the other hand, LCDM is right, one would hope that the big detection experiments (like CDMS) will soon find something. I find it hard to have faith in the existence of hypothetical invisible particles that anybody has yet to detect.

After I wrote this page, Slosar, Melchiorri, & Silk (2005) analyzed the new BOOMERanG data shown above and claim that CDM is more likely than MOND by 200:1. This number depends entirely upon one's prior. I am actually surprised MOND comes off so well, given the sensitivity of such an analysis to the prior probabilities assigned. After years of harping that MOND couldn't make a prediction for the CMB at all (back when no-CDM was the only thing that fit), now some people want to treat the no-CDM prediction as a delta-function prior: even the slightest deviation from the light blue line would be seen as evidence for CDM. If we assign MOND a delta-fcn prior, then it will inevitably look less probable than CDM in this diagram, because CDM has nearly infinite flexibility to fit anything. Yet it is true that MOND does not make this prediction - the corollary of the absence of dark matter does. It is too early yet to say whether TeVeS requires a low third peak or not.

If we were to do this same type of exercise for rotation curves, then we would find MOND to be strongly favored. But that now depends on LCDM's prior for rotation curves, which is not well defined. If we take this to be NFW halos with concentrations predicted by LCDM cosmological parameters, then MOND is more probable by > 1000000:1. If instead we allow for modification of the initial halo profile by feedback, then the answer depends on the particular model. If a model can do as well as MOND, then it will do OK in this test. But this probablistic approach completely misses the much deeper question: why should CDM produce galaxies with rotation curves that look like MOND?