The Third Peak in TeVeS

McGaugh (1999) suggested the no-CDM model as the simplest ansatz that could stand in for a MOND prediction for the microwave background. This simple approach was bound to fail at some level, and I discussed some of the ways in which I expected it to fail. These included early reionization and an enhanced ISW effect, both of which are observed in the WMAP data.

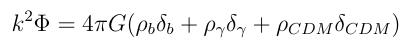
One way I did not expect it to fail was in the pattern of peaks. Without CDM, I reasoned, one should only see the effects of baryonic drag, and therefore each peak should be lower in amplitude than the one before. This worked quite well to predict the ratio of the 1st:2nd peak amplitude. Indeed, it was the only successful a priori prediction of this quantity, which can only be fit with CDM by boosting the baryon density.

The nominal prediction of the simple no-CDM scenario is that the third peak should be lower than the second. This is not observed - the third peak is about the same amplitude as the second peak. Hence the simple no-CDM prediction fails, and in a way which I did not expect. However, we knew it had to fail, so the question becomes:
what does a relativistic theory of MOND actually predict for this?

For the case of TeVeS, this has been worked out by Skordis, Mota, Ferreira, & Boehm. At a conference hosted by SUPA at the ROE, Skordis gave a nice talk outlining TeVeS and Ferreira spelled out its implications for the third peak. In CDM, the perturbations are governed by

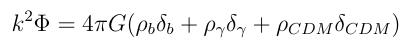
As long as the CDM does not couple to the photons, then fluctuations in the dark matter can grow and it provides a net driving to the oscillations which is otherwise suppressed.

In the case of TeVeS, there is presumably no cold dark matter. But there is a scalar field, phi. The equivalent equation (Skordis et al. 2006) now becomes

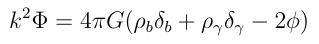
One can see, by inspection, that the scalar field plays the role usually ascribed to CDM of providing a driving term in the oscillations.

Note that this is not a fudge. It hasn't been forced into the theory; it falls out of it. In retrospect, it may even seem more appealing to attribute driving effects to a new field that is part of a grander theory than to a new ad hoc mass component. (Note also that Skordis et al. did publish their paper prior to the release of the third year WMAP data.)

Of course, it may seem no better to invent an invisible scalar field than a new, invisible form of mass. It is important to realize that one has not just invented a new form of dark matter. This can be done in modified gravity theories, with the scalar field term becoming a significant component of the mass-energy tensor. In the case of TeVeS, however, the relic density of the scalar field is tiny. It can still overcome Silk damping and drive significant oscillations because of the way it couples in TeVeS.

That said, it remains to be seen whether a tolerable fit to the WMAP data can be obtained. The authors showed plots at the conference that made it clear it was possible to obtain a third peak comparable to the data, but are still in the process of trying to fit the best cosmic parameters. There is no guarantee that this will work out.

In one sense this is good - a theory that is built to explain one set of phenomena (the MOND phenomenology in galaxies) also naturally predicts a driving term required by an unrelated set of data (WMAP). On the other hand, it is bad. The CMB data themselves may not provide a test capable of distinguishing the possibilities.

While we will have to wait and see what fit is obtained, it seems likely to include a massive neutrino component. This can be reduced by consideration of models wherein the cosmic geometry is not precisely flat, but is likely still to be present. The absolute value of the neutrino mass then becomes a critical test, with a break even point of about 0.5 eV. Above this mass, CDM can not form structure fast enough. Below this mass, one may be stuck with the residual mass discrepancy that plagues MOND in clusters of galaxies.