Large Scale Structure in MOND

1. The gravitating mass density exceeds that of baryons from BBN: Ω_m > Ω_b, and
2. The rich large scale structure observed at z=0 must emerge from the initially smooth initial condition prescribed by the cosmic microwave background at z=1088.

The first point resolves in the usual way in MOND: the conventional gravitating mass is overestimated in the low acceleration regime. After correction for this, Ω_m ≈ Ω_b albeit with large uncertainties (McGaugh & de Blok 1998). We would thus live in a very low density universe. One consequence of this is that the coincidence problem goes away. Indeed, there may be no special value of Ω in MOND because even a very low density universe will eventually recollapse (Felten 1984) [in the absence of some force like dark energy to couteract the stronger long range attraction of MOND].

Addressing the second point, the formation of large scale structure, is a much more challenging problem. Unlike the conventional case in which the growth rate of density perturbations can be solved in an elegant way with linear perturbation theory, the problem is inherently non-linear from the onset in MOND. This makes it difficult to compute structure in MOND and compare the two paradigms fairly.

Indeed, advocates of ΛCDM frequently point to large scale structure as working out so well that it can't possibly be an accident. Of course, those familiar with the evidence for MOND feel the same way about rotation curves. The usual counter to this is that galaxies in ΛCDM are complicated, non-linear objects that have suffered from lots of messy baryonic physics. By extension, we should therefore be absolved of having to understand them. But then the same is true for large scale structure in MOND: the problem is inherently non-linear, the only particles are baryonic so there is no clean dark-matter only version of the problem, and even numerical computations must worry about convergence, probably on Gpc scales, given the enhanced long range nature of the force law.

This is a good example of how topics that are neatly predicted by one paradigm are often a mess in the other.

Nevertheless, we can make some educated deductions as to how structure formation proceeds in MOND (Sanders 1998, McGaugh 1998, McGaugh 1999, McGaugh 2000, Sanders 2001, Nusser 2002, Stachniewicz & Kutschera 2002, McGaugh 2004, Skordis et al. 2005, Llinares et al. 2008, Feix 2016, Khoury 2016, and others):

Initially, at the time of recombination, the universe is very nearly homogeneous. Radiation domination persist until a later epoch than conventionally owing to the lower mass density. Unlike the case of CDM where density perturbations can grow in the dark sector, the initial growth of density perturbations is suppressed until matter domination (z ≈ 200). Once released by the photons, expanding overdensities suddenly find themselves deep in the MOND regime, and act like they have a lot of dark matter. Structure formation proceeds qualitatively as it would conventionally (MOND is, after all, just a boost to Newton), but structure forms harder and faster.

The growth of overdensities in MOND The growth of spherically symmetric over-densities in a low-density baryonic universe as a function of scale factor in the context of a two-field Lagrangian theory of MOND. The solid curves correspond to regions with comoving radii of 20, 40, and 80 Mpc. The dotted line is the corresponding Newtonian growth. With MOND, smaller regions enter the low-acceleration regime sooner and grow to larger final amplitude. The vertical dashed line indicates the epoch at which the cosmological constant begins to dominate the Hubble expansion. [Reproduced from Sanders & McGaugh 2002.]

Structure forms in MOND. Rather than being impossible, structure forms, if anything, too fast: Nusser (2002) finds that it overshoots σ₈ by a factor of two. That is not right, but then again it seems pretty good to get that close on a first try when the total growth factor is a factor of 100,000. Bear in mind that MOND is a highly non-linear theory, and that standard theory (Ω_m = 1 SCDM) missed by a much larger factor at a similar state of development. That was one reason we added Λ.

Here are some predicted consequences of structure formation in MOND:

• Early reionization.
  • Baryons are condensed into structures able to form stars and irradiate the cosmos with UV radiation earlier than in ΛCDM.
  • This predicts the deep 21cm absorption feature seen by EDGES.
• The first L* galaxies form at z ≈ 10.
• The cosmic web emerges early, by z ≈ 4 or 5.
• Rich clusters of galaxies form as early as z ≈ 2.
  • Massive objects like El Gordo arise naturally.
• Large voids are largely swept clear by z ≈ 0.
  • Contrary to the case in CDM, we do not expect large amounts of mass in the voids.
• Large (1,000 km/s) bulk velocities develop naturally (Katz et al. 2013).

Galaxies form in a sort of compressed-timescale bottom-up scenario. Small things form first (this is virtually unavoidable simply on the grounds of dynamical timescales) but merging happens rapidly while the universe is young, so some large galaxies are in place early. This may help understand what has come to be termed downsizing, in which the largest galaxies appear to be the oldest, opposite of what one would naively expect in hiearchical formation scenarios. I speculate that the whole process proceeds more rapidly in high density regions and more slowly in low density regions, so that bright ellipticals form early and low surface brightness galaxies form later. Environment may also play an enhanced role in that galaxies that linger in the cores of galaxy clusters are subject to external fields near to or in excess of a₀. This would remove the disk stability provide by MOND, perhaps driving the transformation of morphology in cluster cores (e.g., Arp 120 in Virgo).

On large scales, the universe may start isotropic and homogeneous (at z=1000) but it need not stay that way. The non-linearity of MOND should cause the development of large scale inhomogeneity that should not happen conventionally. (This is why it is necessary to assume galaxies are biased, so that there can be a lot more dark matter in voids than meets the eye.)

These predictions have been around for some time now, having been discussed in the literature cited above around the turn of the milleneum. More recently, Dodelson (2011) has revisited the linear perturbation problem in TeVeS. While this is an admirable thing to do, this is only one possible relativistic parent theory for MOND, so the results are not general. More importantly, one still needs to account for the nonlinearity of the theory, which can cause mode mixing that washes out the sharp baryonic features that are initially present in the power spectrum. (Compare Dodelson 2011 with McGaugh 1998).

Simulated structure formation in ΛCDM and MOND

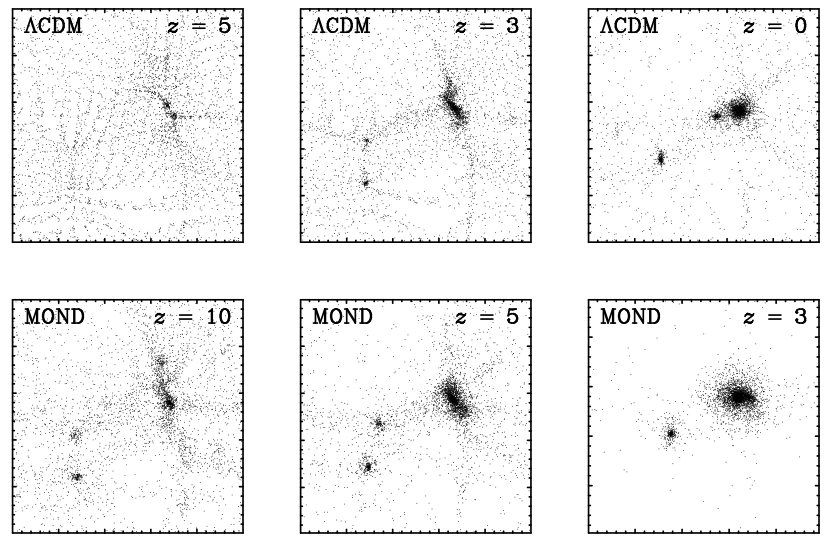
Simulated structure formation in ΛCDM (top) and MOND (bottom) showing the more rapid emergence of simular structures in MOND (note the redshift of each panel).