The modern conception of gravity began in the seventeenth century with Sir Isaac Newton. At the basis of Newton's Universal Law of Gravitation is a simple empirical observation:
Everything happens... as if the force between two bodies is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
- Sir Isaac Newton
This plain fact explained the detailed motion of the moon, encapsulated Kepler's Laws of planetary motion, and in the modern day informs us how to navigate tiny spacecraft through the vast expanses of interplanetary space with remarkable precision. Never in history has any such plainspoken observation carried us (literally!) so far.

Newton's law of gravity has been tested over a wide range of scales, from the submillimeter to the solar system. Its repeated successes and incredible accuracy is rivaled by few other physical theories. The trustworthiness of Universal Gravitation was such that in the nineteenth century the tiny excess precession of Mercury's orbit constituted a crisis.

This crisis was resolved by Einstein's theory of General Relativity, the only significant update to our conception of gravitation since Newton. General Relativity has itself withstood many precision tests. The repeated successes of Newton-Einstein theory, and the sheer eminence of its authors, has led to a widespread attitude among scholars that there can be nothing new to learn about gravitation. Many of these same scholars simultaneously adhere to the contradictory attitude that there must be a unified theory of everything, or at least of the four fundamental forces. So far, gravity has steadfastly refused to be assimilated into the quantum mechanical picture which is essential to the description of the other forces of nature. Yet there must be a quantum theory of gravity. Pursuing this to its logical conclusion, there must be yet more to learn beyond what Newton and Einstein have already told us.

Beyond the quantum realm, there are other gravitational puzzles that remain to be explained. One of the most pertinent is commonly referred to as "the dark matter problem." When astronomers measure the motions of stars and gas in galaxies and yet larger systems, they find that speeds are well in excess of what can be explained by the application of Netwon's Universal Gravitation to the mass in visible forms such as stars (see Figure 1). This has led to the inference that most (roughly 90%) of the mass in the universe is dark.

There is a tremendous amount of evidence for dark matter. Yet all of this evidence is based on the assumption that Newtonian theory can safely be extrapolated from the solar system (where it is well tested) to the scales of galaxies. While an excellent starting point, we should not presume that it will indeed hold. Sticklers for epistemology might object that, strictly speaking, we are faced not with evidence for dark matter, but rather for mass discrepancies. What we see doesn't add up, so either the universe is full of unseen mass, or the theory which leads to the inference of this mass needs revision.

To return to gravity's empirical roots, recall Newton's observation that "everything behaves as if..." While this is true with great accuracy in the solar system, it is patently false in galaxies and other extragalactic systems. If it held, we would have no need for dark matter. Casting the blame instead on gravity might be appropriate if there exists a modification of Newton's formula which satisfies the spirit of his dictum "everything behaves as if..."

Many such attempts have been made, and many have failed. These failures encouraged people in the direction of dark matter. Yet there is one idea which has yes to fail. In 1983, Israeli physicist M. Milgrom hypothesised a specific change in the equations governing particle motions at very low accelerations. He called this the modified Newtonian dynamics, or MOND. MOND reduces to the usual Newtonian form in the regime of high acceleration, but at accelerations lower than 1 part in 10¹¹ of what we feel here on earth, things change in a way that might account for the mass discrepancy.

Once the equations of MOND (or any other hypothesised modification) are written down, they leave little room for maneuver. Accurate dynamical data, such as the rotation curves of spiral galaxies, must follow from the application of MOND to the observed distribution of luminous matter (stars and gas). Each and every galaxy provides a unique test of the hypothesis. Fits to the observed rotation curves of galaxies like that in Fig. 1 have now been performed for over 100 galaxies, with comparable results. While there is certainly the occasional puzzle, there are no known cases where MOND clearly fails. In the vast majority, it clearly succeeds. MOND is the formula which satisfies Newton's dictum "everything behaves as if..."

In his original 1983 papers, Milgrom made a series of predictions about a then unknown class of 'low surface density' galaxies. These objects should, if MOND is correct, exhibit large mass discrepancies because their diffuse luminous mass would provide an even weaker gravitational acceleration than the already tenuous amount found in brighter galaxies. He listed a number of specific, testable consequences of this prediction. At the time, such objects were thought to be rare or nonexistent. Later they were discovered, and are now known as 'low surface brightness' galaxies. In the process of studying these new objects for their own interest, astronomers gradually accumulated the data necessary to test Milgrom's largely forgotten, decade old predictions. It came as quite a shock to find that every one of them was realised in the data. While science in principle advances by the construction of hypotheses that make predictions which can subsequently be tested, it is a rare case indeed that in practice actually follows this model so cleanly.

These successes of MOND are most obvious in places where the dynamical data which test it are most accurate. However, there are many other systems where the picture is less clear. Any modification of dynamical laws must explain the mass discrepancy everywhere. It must work not only for rotation curves, but also for the velocity dispersions of spheroidal galaxies, the gas temperatures of clusters of galaxies, and the peculiar motions of galaxies in the large scale structure of the universe.

One place MOND appears to have serious difficulties is in rich clusters of galaxies: the luminous mass falls short by a factor of roughly two of what is needed to explain the observations. On the one hand, this may not seem so bad: coming within a factor of two in astronomy is often viewed as a great success. On the other hand, the discrepancy does appear genuine. This implies that there remains some additional mass yet to be discovered in clusters. This, in effect, invokes some form of dark matter - hardly a selling point for a theory which seeks to do away with such stuff. This might be considered fatal for MOND were it not for the fact that the discovery of huge reservoirs of mass in clusters has happened before. It was long thought that the stars in the galaxies which made up the clusters were the biggest reservoir of normal matter there. About a decade ago, it became apparent that the mass of hot, diffuse gas spread between the cluster galaxies greatly exceeds the mass in stars. This being the case, it is hard to be confident that another factor of two won't turn up.

Another problem is cosmology. Unmodified General Relativity provides a satisfactory interpretation for the empirical aspects of the hot big bang cosmology - an expanding universe, nucleosynthesis of the light elements, and the relic radiation known as the cosmic microwave background. The success of standard cosmology is often equated with evidence against MOND. Yet the standard cosmology is only viable if 90% of the mass indeed exists in an as yet hypothetical form - hardly a great boasting point. Worse, in recent years it has become necessary to revive Einstein's self-described "greatest blunder": the cosmological constant. One might wonder if these strange turns are hinting at some greater truth.

The cosmic microwave background may help to decide this issue. A universe full of dark matter leaves a subtly different signature on this echo of the big bang than does one devoid of dark matter. Recent observations came tantalizingly close to being able to distinguish between the two cases, but ultimately failed to make a clear distinction. Upcoming space missions, like NASA's MAP and ESA's PLANCK, will hopefully do the trick.

Regardless of whether MOND is correct as a theory, it does constitute an observed phenomenology which demands explanation. Herein lies a real conundrum for the dark matter picture. The natural expectations of dark matter theories for rotation curves do not look like MOND, and hence fail to reproduce a whole set of essential observational facts. The best a dark matter theory can hope to do is contrive to look like MOND, and hence postdict the many things which Milgrom successfully predicted. This gives one genuine pause to consider how science is suppose to proceed.

The debate between dark matter and MOND is refreshing. There has been some concern expressed in recent years that science is at its end. All the fundamental discoveries have been made; there is nothing truly new left to discover. This sentiment echoes the words of Rutherford nearly a century ago: "All that remains... is to fill in the last few decimal points." Now, as then, the rumors of the end of fundamental science are greatly exaggerated.

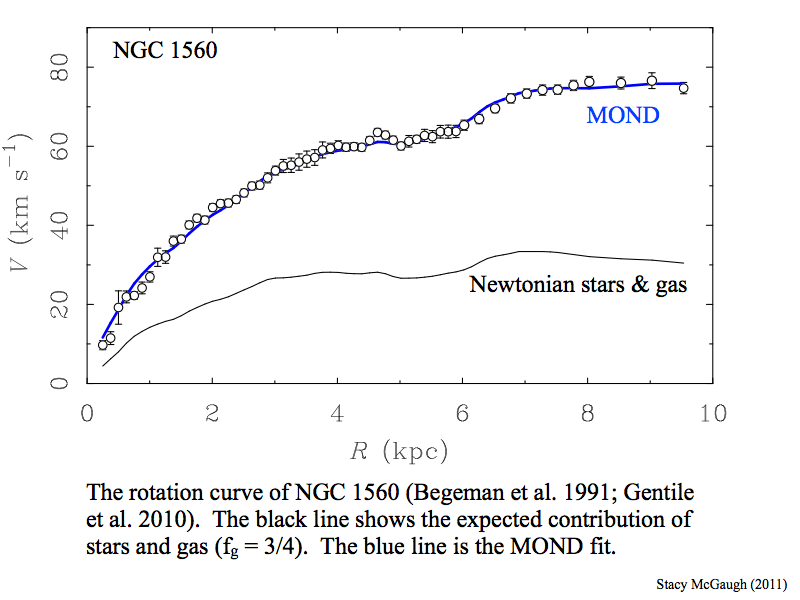
Figure 1: The rotation curve of the dwarf galaxy NGC 1560. The lower line is the rotation predicted by the application of Newtonian gravity to the observed stars and gas. This falls well short of the observed rotation, leading to the inference of dark matter to make up the difference. The upper line shows the rotation is expected by the application of MOND to the observed stars and gas. Similar results are now known for over 100 galaxies. Note that in this case, even the kink observed in the gas distribution is reflected in the rotation. This is exceedingly difficult to explain with dark matter which is not distributed like the luminous mass. MOND is the formula which satisfies the Newton's dictum "everything behaves as if..."

Translated into Polish
Translated into Russian
Translated into Ukrainian
Translated into Portuguese
Translated into Romanian courtesy of Essay Writing Services
Translated into Dutch once here and again here
Translated into Georgian
Translated into Azerbaijanian
This page has been translated into Swedish by Eric Karlsson
Translated into Urdu
Translated into Norwegian
Translated into Marathi