ASTR 333/433 - Dark Matter
Homework 3 - Due at the beginning of class November 8

Late homework suffers a 20% penalty
Further depreciation occurs for every additional day late

  1. Brown dwarf MACHOs

    1. Early on, brown dwarfs were a popular dark matter candidate. Presuming that the typical brown dwarf has a mass of 0.02 M☉, and recalling the result for the local density of dark matter from the first homework (0.006 M☉pc-3), what local number density would be required for brown dwarfs to be the dark matter in the Milky Way? What is the corresponding separation between these brown dwarfs?

    2. The optical depth τ of gravitational lensing for MACHOs in the halo is

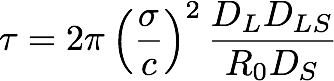
      What is the optical depth τ to gravitational lensing from a halo of brown dwarfs in the direction of the LMC?

      We are 8 kpc from the Galactic Center; the LMC is 50 kpc away. Where is the typical lens? The typical speed of a brown dwarf in the halo would be σ = V/√3 = 100 km/s.

    3. The observed limit found by EROS is τ < 3.6 x 10-8. How does this compare with the optical depth you computed? What does this imply?

    4. The EROS limit only applies for objects of mass > 10-8 M☉. What famous solar system object has about this mass? What local number density and typical separation would such objects have if they were to be the dark matter? Would we notice them?

      ASTR 433 only:

    5. How does the kinetic energy of a 10-8 M☉ dark matter object compare with the gravitational binding energy of the Earth?

  2. Milky Way baryons

    The dark matter halo of the Milky Way can be crudely approximated as an NFW halo with c = 8 and V200 = 162 km/s.

    1. What is the "total" mass of the Milky Way, M200?
      Recall from the last homework that M200 = 3.3 x 105 (V200)3.
    2. According to fits to the cosmic microwave background, the cosmic baryon fraction fb = Ωb/Ωm = 0.16. Given this, what should the baryonic mass of the Milky Way be?
    3. The tally of known stars and gas is approximately 7.4 ± 0.3 x 1010 M☉. How does this compare with the mass you obtained in (ii)?
    4. Miller & Bregman (2015) estimate that in additoin to the stars and cold gas in the disk of the Milky Way (within 20 kpc), there may be some additional hot coronal gas around the Milky Way at larger radius (but within R200). This extra gas might have a mass of 4.3 ± 0.9 x 1010 M☉. How would this impact the answer to (iii)? Do the stated uncertainties suffice to resolve any tension that might be present?

  3. X-ray gas in the Coma Cluster

    Coma is the most massive "local" cluster at a distance of 100 Mpc. It has an ICM temperature TX = 90 million K. (Toasty, eh?)
    1. Assuming the ICM gas is contained in hydrostatic equilibrium, what is the mass enclosed within 1 Mpc of the cluster center?
      You may assume that the gas is isothermal and that the density profile is that of the inner part of an NFW halo. The mean molecular weight is 0.62 [= 1/(2X+0.75Y+0.5Z)].
    2. What is the characteristic velocity corresponding to this mass?
      [Hint: remember, V2 = GM/r.]
    3. If a galaxy far in the background (1.1 Gpc) is gravitationally lensed by this mass, what is the angle of the arc it makes?
      This is referred to in the notes as θI, not the bend angle αd.

  4. Ωm from Cluster Baryon Fractions

    Use these data from Gonzalez et al. (2013) to answer this question. Read the data file, paying close attention to the units.
    1. Plot the fraction of gas, stars, and total baryons as a function of mass. Are stars or gas more important to the total baryonic mass? Can you discern a trend in these quantities with mass?
    2. Combine the mean baryon fraction from (i) with the Big Bang Nucleosynthesis constraint Ωb h2 = 0.022 to estimate the mass density of the universe Ωm. You may assume h = 0.7.
    3. How does this compare with the universal baryon fraction obtained from fits to the cosmic microwave background, fb = 0.16? Why might they differ?
    Historically, the baryon content of clusters was an important line of evidence contradicting the cosmic orthodoxy that Ωm = 1. (That's Ωm, not Ωtot.)

  5. Timing Argument

    Andromeda is 770 kpc away from the Milky Way and approaching us at 120 km/s. Lets assume that these two most massive galaxies of the Local Group (having a total mass m+M) started out expanding away form each other with the Hubble flow but are now falling together on a perfectly radial orbit (e = 1).


    Traditionally one assumes an age for the universe (t0) in order to solve for η. That's a tad tedious, so instead accept that η=4.2 and determine
    1. the semimajor axis a
    2. the age t0
    3. the total mass m+M
    4. the time to when Andromeda crashes into us.
    5. the mass-to-light ratio of the Local Group.
      The luminosity of Andromeda is 7.1 x 1010 L☉ and that of the Milky Way is 4.1 x 1010 L☉. You may neglect the rest of the Local Group, as the other galaxies contribute little to the total luminosity (see McConnachie 2012)).
    6. is dark matter required?

      ASTR 433 only: Now suppose the orbit is not perfectly radial, but still pretty eccentric. The development parameter doesn't change* much from the e = 1 case.

      Adopting e = 0.8 and η = 4.3 for an age of 13.2 Gyr, determine the semi-major axis a of the orbit.

    7. Will M31 collide with the Milky Way now?
      Assume their centers require a clearance of 100 kpc for safe passage. That's twice the distance to the Magellanic Clouds. Recall that the pericenter = a(1-e).
    8. Does the implied mass increase or decrease?
    9. Do either of these changes (to a and m+M) seem so dramatic that they would be readily obvious?

      *This is not part of the assignemnt, but if you're curious: to see that the development parameter is not too sensitive to e for large e, it is instructive to plot f(η) = (dr/dt)/(r/to) = e sin(η)(η-e sin(η)/(1-e cos(η))2.