Brown dwarf MACHOs
- Early on, brown dwarfs were a popular dark matter candidate.
Presuming that the typical brown dwarf has a mass of 0.02 M☉,
and recalling the result for the local density of dark matter from the
first homework (0.015 M☉pc-3),
what local number density would be required for brown
dwarfs to be the dark matter in the Milky Way? What is the corresponding separation
between these brown dwarfs?
- The optical depth τ of gravitational lensing for MACHOs in the halo is
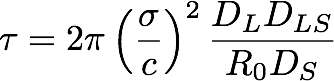
- What is the optical depth τ to gravitational lensing from a halo of brown dwarfs
in the direction of the LMC?
Hint: We are 8 kpc from the Galactic Center; the LMC is 50 kpc away. Where is the typical lens? What is its typical speed (σ)? - The observed limit found by EROS
is τ < 3.6 x 10-8. How does this compare with the optical depth you computed?
What does this imply?
- The EROS limit only applies for objects of mass > 10-8 M☉.
What famous solar system object has about this mass? What local number density and
typical separation would such objects have if they were to be the dark matter?
Would we notice them?
ASTR 433 only:
What would the kinetic energy of such a 10-8 M☉ halo object should it happen to collide with the Earth? How does this compare with the gravitational binding energy of the Earth?
Milky Way baryons
Suppose the rotation curve of the Milky Way stays flat at 220 km/s out to the "edge" of the dark matter halo at 180 kpc.
- What is the dynamical mass of the Milky Way within this edge?
- What is the detected baryon fraction of the Milky Way?
The tally of known stars and gas is approximately 5 x 1010 M☉. - If the cosmic baryon fraction fb = Ωb/Ωm = 0.15, what mass of baryons is missing?
- Speculate on the current location & state of the missing baryons.
i.e., where are they now? what form are they in?
The Coma Cluster
Coma is the most massive "local" cluster at a distance of 100 Mpc. It has an ICM temperature TX = 90 million K. (Toasty, eh?)- Assuming the ICM gas is contained in hydrostatic equilibrium,
what is the mass enclosed within 1 Mpc of the cluster center?
You may assume that the gas is isothermal and that the density profile is that of the inner part of an NFW halo. The mean molecular weight is 0.62 [= 1/(2X+0.75Y+0.5Z)]. - What is the characteristic velocity corresponding to this mass?
[Hint: remember, V2 = GM/r.]- If a galaxy far in the background (1.1 Gpc) is gravitationally lensed by this mass, what is the angle of the arc it makes?
Ωm from Cluster Baryon Fractions
Use the data in the table (from White & Fabian 1995) to compute the baryon fractions of these clusters (you may neglect stars, presuming the gas mass is most of the baryons). If Big Bang Nucleosynthesis tells us the baryon density Ωb h2 = 0.02, and assuming that clusters represent a fair sampling of the universe, what is Ωm?How does your answer depend on the Hubble constant?
Is the scatter in fb consistent with the quoted errors?
[It may help to make a plot of some relevant quantities.]
| Cluster | Mgas | ErrMgas | Mtot |
| A85 | 0.87 | 0.06 | 4.64 |
| A401 | 1.32 | 0.07 | 10.1 |
| A478 | 2.38 | 0.21 | 9.28 |
| A545 | 1.91 | 0.25 | 10.6 |
| A644 | 0.95 | 0.06 | 9.06 |
| A665 | 4.37 | 0.46 | 22.1 |
| A1413 | 1.83 | 0.23 | 15.9 |
| A1650 | 0.75 | 0.08 | 6.37 |
| A1689 | 2.12 | 0.16 | 15.5 |
| A1763 | 2.61 | 0.22 | 13.2 |
| A1795 | 1.13 | 0.08 | 5.49 |
| A2009 | 1.44 | 0.10 | 10.6 |
| A2029 | 1.26 | 0.11 | 10.3 |
| A2142 | 2.84 | 0.15 | 20.1 |
| A2163 | 5.46 | 0.49 | 32.5 |
| A2319 | 1.73 | 0.12 | 14.2 |
| A3186 | 1.76 | 0.23 | 9.50 |
| A3266 | 1.42 | 0.07 | 9.07 |
| A3888 | 1.20 | 0.15 | 8.66 |
These data assume H0 = 50 km s-1 Mpc-1.
Mgas and Mtot are in units of 1014 Mo.
Mgas scales as h^-5/2 (roughly),
Mtot as h^-1.
Timing Argument
Andromeda is 770 kpc away from the Milky Way and approaching us at 120 km/s. Lets assume that these two most massive galaxies of the Local Group (having a total mass m+M) started out expanding away form each other with the Hubble flow but are now falling together on a perfectly radial orbit (e = 1).
| Eine kleine orbit theory |
|---|
| The position of an object r(t) along an orbit can be described by the development
parameter η such that
r = a[1-e cos(η)] t = {a3/[G(m+M)]}1/2 [η-e sin(η)]
where e is the eccentricity of the orbit and a is the semimajor axis.
dr/dt = (dr/dη)/(dt/dη) =
{[G(m+M)]/a}1/2 e sin(η)/[1-e cos(η)] (see the end of chapter 4 of Sparke & Gallagher). |
Traditionally one assumes an age for the universe (t0) in order to solve for η. That's a tad tedious, so instead accept that η=4.2 and determine
- the semimajor axis a
- the age t0
- the total mass m+M
- the time to when Andromeda crashes into us.
- the mass-to-light ratio of the Local Group.
The luminosity of Andromeda is 2.7 x 1010 L☉ and that of the Milky Way is 1.5 x 1010 L☉. You may neglect the rest of the Local Group (see Table 4.1 of Sparke & Gallagher). - is dark matter required?
ASTR 433 only:
Now suppose the orbit is not perfectly radial, but still pretty eccentric.
The development parameter doesn't change much from the e = 1 case.
Adopting e = 0.8 and η = 4.3 for an age of 13.2 Gyr,
determine the semi-major axis a of the orbit.
Assume their centers require a clearance of 100 kpc for safe passage.
That's twice the distance to the Magellanic Clouds.
Recall that the pericenter = a(1-e).