Cosmic Microwave Background Radiation

• What is the number density of photons?

• If the mean mass density of baryons in the universe is ρ₀ = 2 x 10^-31 g cm^-3, what is the number density of baryons?

• What is the baryon-to-photon ratio?
  

WIMPs in you

• Assuming the dark matter is made of WIMP mass of 107 GeV with a local density of 0.3 GeV cm^-3, how many are passing through your body at any given moment?
  [Hint: your volume follows easily from assuming that you have the density of water.]

WIMP Detection

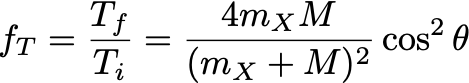
where θ is the scattering angle. A common target nucleus is Xenon, with M = 123 GeV. Assuming that the typical speed of a WIMP in the Milky Way halo is 130 km/s,

• What is the kinetic energy of a WIMP of mass m_X = 107 GeV?
• What fraction of the kinetic energy is transferred to the Xenon nucleus in a head on collision (cos θ = 1)?
• The minimum WIMP mass is set be the Lee-Weinberg limit to be at least 2 GeV. What is the maximum fraction of energy transferred if WIMPs happen to be at this limiting mass?
• What do your answers tell you about how the sensitivity of dark matter detectors depend on the mass of the WIMP and the target nuclei?

Predicting dwarf galaxy velocity dispersions

Suppose the Milky Way is discovered to have a new dwarf satellite galaxy with the following properties:

D = 200 kpc

Re = 1 kpc

M* = 105 M☉

A colleague proposes to observe this system to measure its velocity dispersion. Can you predict what she will see?

Method 1: Newton

• Use the virial relation to predict the velocity dispersion assuming that the only mass present is that of the stars.

  Method 2: Abundance Matching:
  Fig. 6 of the review by Bullock & Boylan-Kolchin (arXiv:1707.04256) shows the relation between stellar mass and halo mass (and V_max of the halo) obtained from abundance matching. Use this graph to

• Estimate the halo mass and the range of plausible halo masses.
• Estimate the corresponding velocity dispersion and its range.
  [You may assume σ = V_max/√3]
• For this velocity, compute the dynamical mass and the ratio of dynamical to stellar mass.
• Is this mass consistent with the halo mass? If not, why not?

  Method 3: MOND
  The velocity dispersion estimator for an isolated object in the deep MOND regime is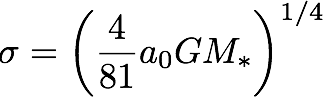

  

  [You can find the value of a₀ on the useful numbers page.]

• What is the velocity dispersion predicted by MOND for this system, assuming it is isolated?
• Check that this dwarf is in the MOND regime.
  [This formula applies only for very low accelerations, when the internal acceleration g_in = 3 σ²/r_1/2 is less than a₀.]
  [The 3D half-light radius r_1/2 is commonly assumed to be (4/3) times the measured projected (2D) effective radius: r_1/2 = (4/3) R_e.]

  Distinguishing the predictions:
  The best observational accuracy that is typically obtained for the velocity dispersion in such systems is ± 2 km/s.

• Should it be possible to distinguish between the hypotheses above?

  ASTR 433 only:

  Method 4: the External Field Effect
  A unique feature of MOND is the external field effect (EFE). When the external field g_ex of the host exceeds the internal field of the dwarf satellite, the velocity dispersion estimator becomes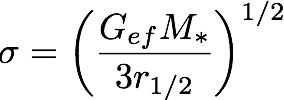

  

  where G_ef ≈ (a₀/g_ex)G. This quasi-Newtonian regime has a higher effective value for Newton's constant.
  

• Is this dwarf in the isolated or quasi-Newtonian regime?
  I.e., is g_in > g_ex or g_in < g_ex?
  [To estimate g_ex, assume the rotation curve of the Milky Way remains flat at 200 km/s.]
• What is the velocity dispersion predicted for this system considering the EFE?
• Can this be distinguished from the isolated case?

Donkey Dark Matter

Professor Mihos once jokingly speculated that the dark matter could be composed of free floating space donkeys (FFSDs).
Can we constrain this possibility?

Live Donkeys

FFSDs would not radiate in the optical, but would emit in the infrared (presuming they have space suits to keep them at a comfortable body temperature of 37 C). If the halo mass of a typical L* (≈ 2 x 10¹⁰ L_☉) galaxy is 10¹² M_☉, what is its infrared luminosity? How does this compare to its optical luminosity? Could we detect this? (Bear in mind that while IR detector technology lags behind optical detector technology, it has nevertheless gotten pretty good).

It may help to recall the Wien and Stefan-Boltzmann Laws. To estimate plausible donkey parameters you may assume a spherical donkey.

ASTR 433 (required); ASTR 333 (extra credit):

Dead Donkeys

FFDDs (Free Floating Dead Donkeys - those lacking space suits) would quickly come into thermal equilibrium with the CMB and any other stray energy sources, making them much harder to detect. They would occasionally collide with the Earth.
Recalling that the collision rate is the product N σ V (number density, cross-section, and relative velocity), compute

• the approximate frequency of FFDD impacts on the Earth.
• the kinetic energy deposited by each impact.

Would we notice this?