ASTR 333/433 - Dark Matter
Homework 4 - Due at the beginning of class April 18

  1. WIMPs in You

    Assuming the dark matter is made of WIMPs with a mass of 107 GeV with a local density of 0.3 GeV cm-3, how many are passing through your body at any given moment?
    [Hint: your volume follows easily from assuming that you have the density of water.]

  2. WIMP Detection Channels

    Sketch a feynman diagram for the interaction of WIMPs with Standard Model particles and use it to describe the three channels available for WIMP detection.

  3. WIMP Direct Detection

    Direct WIMP detection experiments are predicated on detecting the kinetic energy deposited by WIMPs scattering off atomic nuclei.
    For elastic scattering, the fraction of the initial kinetic energy Ti transferred from a WIMP of mass mX to a nucleus of mass M is

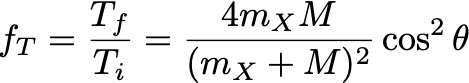
    where θ is the scattering angle. A common target nucleus is Xenon, with M = 123 GeV. Assuming that the typical speed of a WIMP in the Milky Way halo is 130 km/s,

    1. What is the kinetic energy of a WIMP of mass mX = 107 GeV?
    2. What fraction of the kinetic energy is transferred to the Xenon nucleus in a head on collision (cos θ = 1)?
    3. The minimum WIMP mass is set by the Lee-Weinberg limit to be at least 2 GeV. What is the maximum fraction of energy transferred if WIMPs happen to be at this limiting mass?
    4. What do your answers tell you about how the sensitivity of dark matter detectors depend on the mass of the WIMP and the target nuclei?

  4. The accleration scale in the data

    The radial acceleration relation indicates the present of an acceleration scale g† = 1.2 × 10-10 m/s/s.
    Such a scale is also indicated by the Baryonic Tully-Fisher Relation (BTFR) and the Central Density Relation (CDR). Are these consistent?

    1. BTFR: The quantity gTF = ζ Vf4/(G Mb) defines a line of constant acceleration in the Tully-Fisher plane.
      1. Compute gTF and plot it against baryonic mass Mb for these galaxies.
        Use the same formula for the baryonic mass that you used in part (ii) of Problem 4 in Homework 1.
      2. Are the data consistent with a single value of gTF for all galaxies?
      3. What is the average acceleration, ‹ gTF ›?
      4. Is ‹ gTF › consistent with the value g† from the RAR?

      Note: Flattened disks rotate faster than the equivalent spherical mass distribution, leading to one of those geometric factors of order unity. You may adopt ζ = 0.8, which is a reasonable approximation for realistic finite thickness disks.
      ASTR 433 only: derive and plot the value of ζ as a function radius for a thin exponential disk by comparing it to the spherical disk approximation. (Recall Problem 5 of Homework 1).

    2. CDR: For this part, use these data, which given the central dynamical surface density (Sdyn) and central stellar surface density (Sstar) for SPARC galaxies.
      1. Plot Sdyn vs. Sstar. Judging by eye, at what surface density does the relation bend?
      2. MOND predicts that the high surface density regime should be Newtonian, with Sdyn = Sstar. Is this true in the data? Need it be true in a universe made of dark matter?
      3. MOND predicts that the low surface density regime should follow Sdyn = (4 ΣM Sstar)1/2, where ΣM = a0/(2 π G) [see Milgrom (2016)]. Find the best fit value of ΣM for Sstar < 400 M☉ pc-2. Why this limit? Consider the prediction, look at your graph, and compare to your eyeball estimate in (i).]
      4. Convert your best fit ΣM into the acceleration a0. Is it consistent with the value g† from the RAR?

    3. Comment on the extent to which these three methods, the RAR, BTFR, and CDR, are independent of one another. Are they consistent with being the same value? Should they be? Consider both a dark matter and MOND universe.

  5. Predicting dwarf galaxy velocity dispersions

    Suppose the Milky Way is discovered to have a new dwarf satellite galaxy with the following properties:
    D = 200 kpcRe = 1 kpc M* = 105 M☉
    A colleague proposes to observe this system to measure its velocity dispersion. Can you predict what she will see?

      Method 1: Newton
    1. Use the virial relation to predict the velocity dispersion assuming that the only mass present is that of the stars.

      Method 2: Abundance Matching:
      Fig. 6 of the review by Bullock & Boylan-Kolchin (arXiv:1707.04256) shows the relation between stellar mass and halo mass (and Vmax of the halo) obtained from abundance matching. Use this graph to

    2. Estimate the halo mass and the range of plausible halo masses.
    3. Estimate the corresponding velocity dispersion and its range.
      [You may assume σ = Vmax/√3]
    4. For this velocity, compute the dynamical mass and the ratio of dynamical to stellar mass.
    5. Is this mass consistent with the halo mass? If not, why not?

      Method 3: MOND
      The velocity dispersion estimator for an isolated object in the deep MOND regime is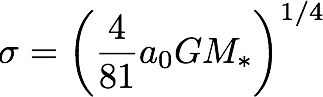

      [You can find the value of a0 on the useful numbers page.]

    6. What is the velocity dispersion predicted by MOND for this system, assuming it is isolated?
    7. Check that this dwarf is in the MOND regime.
      [This formula applies only for very low accelerations, when the internal acceleration gin = 3 σ2/r1/2 is less than a0.]
      [The 3D half-light radius r1/2 is commonly assumed to be (4/3) times the measured projected (2D) effective radius: r1/2 = (4/3) Re.]

      Distinguishing the predictions:
      The best observational accuracy that is typically obtained for the velocity dispersion in such systems is ± 2 km/s.

    8. Should it be possible to distinguish between the hypotheses above?

      ASTR 433 only:

      Method 4: the External Field Effect
      A unique feature of MOND is the external field effect (EFE). When the external field gex of the host exceeds the internal field of the dwarf satellite, the velocity dispersion estimator becomes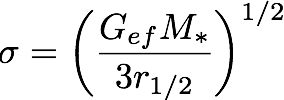

      where Gef ≈ (a0/gex)G. This quasi-Newtonian regime has a higher effective value for Newton's constant.

    9. Is this dwarf in the isolated or quasi-Newtonian regime?
      I.e., is gin > gex or gin < gex?
      [To estimate gex, assume the rotation curve of the Milky Way remains flat at 200 km/s.]
    10. What is the velocity dispersion predicted for this system considering the EFE?
    11. Can this be distinguished from the isolated case?