Astronomical Magnitude Systems
Contents:
This page assumes you understand the astronomical magnitude system.
For a minimalist definition, see the Photometry section of the
useful numbers page.
See also this
more expansive discussion,
with lots of other interesting information.
Definitions of astronomical magnitude systems:
- The Virtual Observatory Filter Profile Service
- A major review of astronomical magnitude systems and their calibration
is given by
- Bessel, M. S. 2005, ARA&A,
43, 293
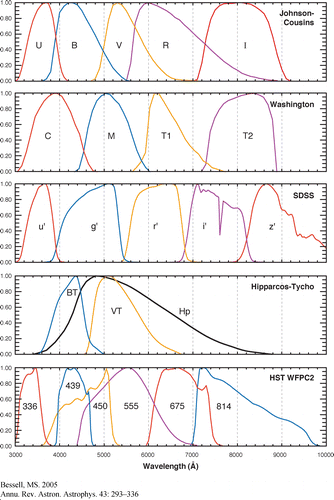
- Johnson System
- This system is defined such that the star Alpha Lyr (Vega) has
V=0.03 and all colors equal to zero. Alternatively, the zero-color
standard can be defined to be the mean of a number of unreddened A0 V
stars of Pop I abundance, using the ensemble of Johnson-Morgan
standards to fix the flux scale. It remains to calibrate on an
absolute scale the flux of Alpha Lyr or some other appropriate star.
Such a aclaibration has been accomplished by Hayes and Lathan (1975),
which yielded 3500 Jansky at 5556Å for Alpha Lyr.
Articles discussing the UBVRI passbands include Bessel (1979), Bessel
(1983), and Bessel (1990).
References:
- Bessel, M. S. 1990, PASP, 91, 589
- Bessel, M. S. 1983, PASP, 95, 480
- Bessel, M. S. 1990, PASP, 102, 1181
- Hayes, D. S., & Latham, D. W. 1975, ApJ, 197, 593
- Johnson, H. L. & Morgan, W. W. 1953, ApJ, 117, 313
- In practice, while observing, one monitors groups of standard stars
such as those tabulated by Landolt:
- Landolt, A. U. 1992, AJ, 104, 340
- Landolt, A. U. 1983, AJ, 88, 439
- Landolt, A. U. 2007, AJ, 133, 2502
- Various observatories have posted electronic versions
of the Landolt standards, e.g.,
- Lick |
WIYN |
CFHT
- these are of course derivative products and one should always check
their veracity against the original work by Landolt.
- Filters: UBVRIJHK
The original Johnson system consists of the UBV filters whose calibration
was intimately tied to the photoelectric detectors in use at the time.
The system has since been extended to the red with optical RI and near-infrared
JHK filters. The definitions of these filters are not always independent of
the detectors involved and can vary slightly fmor observatory to observatory.
- JHK:
The filters JHK are an important extension of the Johnson
system to near-infrared wavelengths. Technology requires different detectors
for these wavelengths than UBVRI, so different calibration stars are required
(Landolt's standards are useful for optical UBVRI observations).
The JHK filters have been used in the
2MASS all sky survey.
Since 2MASS
is (in principle) completely and uniformly calibrated,
any non-variable object in the sky (its coverage is nearly complete)
can (in principle!) be used as a calibration reference.
Note that 2MASS uses a "short" K filter which is slightly different from
the original definition of K but is now in common uses because of its
superior suppression of thermal terrestrial emission.
- Gunn griz System
- This was originally defined in terms of photoelectric detectors
(Thuan & Gunn 1976; Wade et al. 1979), but is now used primarily
with CCDs (Schneider, Gunn, & Hoessel 1983; Schild 1984). The
griz system is defined by a few dozen standard stars, and the star
BD+17deg4708, a subdwarf F6 star with B-V=0.43, is defined to have
colors equal to zero. The absolute calibration of this system is
simply the monochromatic flux of the star (Oke & Gunn 1983),
scaled from g=9.50 to g=0.0, at the effective wavelengths of the griz
bands. A number of detailed aspects of broad-band photometry in the
specific context of measurements of galaxies at large redshifts are
reviewed in Schneider, Gunn, & Hoessel (1983).
References:
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713
- Schild, R. 1984, ApJ, 286, 450
- Schneider, D. P., Gunn, J. E., & Hoessel J. G. 1983, ApJ,
264, 337
- Thuan, T. X., & Gunn, J. E. 1976, PASP, 88, 543
- Wade, R. A., Hoessel, J. G., Elias, J. H., Huchra, J. P. 1979, PASP, 91, 35
- The Gunn-Thuan griz system is employed by the
Sloan Digital Sky Survey.
Since the SDSS is (in principle) completely and uniformly calibrated,
any non-variable object in the large swath of sky it covers could
(in principle!) be used as a calibration reference.
- AB magnitude System
- This magnitude system is defined such that, when monochromatic
flux f_nu is measured in erg sec^-1 cm^-2 Hz^-1,
m(AB) = -2.5 log(f_nu) - 48.60
where the value of the constant is selected to define m(AB)=V for a
flat-spectrum source. In this system, an object with constant flux
per unit frequency interval has zero color.
It is helpful to bear in mind the identity
lambda*f_lambda = nu*f_nu
so
f_nu = f_lambda*(lambda/nu) = f_lambda*lambda^2/c.
References:
- Oke, J.B. 1974, ApJS, 27, 21
- STMAG system
- This magnitude system is defined such that an object with
constant flux per unit wavelength interval has zero color.
It is used by the Hubble Space Telescope photometry packages.
References:
- Stone, R.P.S. 1996, ApJS, 107, 423
The Absolute Magnitude of the Sun:
See also the
more recent and more complete compilation
of Willmer (2018).
| Filter | M⊙ | Source |
| U | 5.61 | B&M |
| B | 5.48 | B&M |
| V | 4.83 | B&M |
| R | 4.42 | B&M |
| I | 4.08 | B&M |
| J | 3.64 | B&M |
| H | 3.32 | B&M |
| K | 3.28 | B&M |
| K' | 3.27 | * |
| WISE | | |
| W1 3.4μ | 3.26 | |
| Spitzer | | |
| 3.6μ | 3.24 | Oh |
| 4.5μ | 3.27 | Oh |
| SDSS | | |
| u | 6.55 | S&G |
| g | 5.12 | S&G |
| r | 4.68 | S&G |
| i | 4.57 | S&G |
| z | 4.60 | S&G |
B&M = Binney & Merrifield
S&G = Sparke & Gallagher
Oh = Oh et al (2008) AJ, 136, 2761
*My (SSM 2007) estimate for the K' filter used by 2MASS after long and painful hunting through the calibration literature.
Casagrande et al. (2012) find exactly the same thing for 2MASS Ks (3.27) while tweaking the other IR colors in minor ways. Others claim the absolute magnitude of the sun in 2MASS Ks is
3.29 or
3.295.
Note that the absolute magnitude of the sun is uncertain by typically 0.03 mag.
in most bands. The "right" answer depends on whether we're talking about the
sun itself, the mean of solar type stars, or stellar atmosphere models.
A shocking number of calibrations seem to depend on the latter. As best I can
tell, this is the difference between 3.27 (for solar analogs, i.e., the average
of solar metallicity G2 V stars) and 3.295 (model stellar atmospheres).
Indeed, I would like for someone to tell me the right I-band absolute magnitude of
the sun. I have seen estimate ranging from 4.08 (above) to 3.9.
Ramirez et al.
give B-V = 0.65 which agrees with the Binney & Merrifield B-V
above, but they find V-I = 0.70 which implies
M⊙I = 4.13.
Update: Willmer (2018) gives 4.10.
See also This alternate opnion, listing
AB absolute magnitudes as well as Vega.
See also this tabulation used by EZgal which gives AB absolute magnitudes and conversions to the Vega system.
See also the Virtual Observatory
Filter Profile Service,
complete with zero points in Janskys.
See also Chris Willmer's page on the
absolute magnitude
of the sun.
Infrared colors of solar-type stars:
| Band | Color |
| V-J | 1.158 |
| V-H | 1.484 |
| V-K' | 1.545 |
| V-[8] | 1.591 |
| V-[24] | 1.590 |
From Table 3 of
Rieke et al (2008).
No guarantee is made about the consistency between this and the above table.
Conversions among magnitude systems:
- Conversion from AB magnitudes to Johnson magnitudes:
- The following formulae convert between the AB magnitude systems
and those based on Alpha Lyra:
V = V(AB) + 0.044 (+/- 0.004)
B = B(AB) + 0.163 (+/- 0.004)
Bj = Bj(AB) + 0.139 (+/- INDEF)
R = R(AB) - 0.055 (+/- INDEF)
I = I(AB) - 0.309 (+/- INDEF)
g = g(AB) + 0.013 (+/- 0.002)
r = r(AB) + 0.226 (+/- 0.003)
i = i(AB) + 0.296 (+/- 0.005)
u' = u'(AB) + 0.0
g' = g'(AB) + 0.0
r' = r'(AB) + 0.0
i' = i'(AB) + 0.0
z' = z'(AB) + 0.0
Rc = Rc(AB) - 0.117 (+/- 0.006)
Ic = Ic(AB) - 0.342 (+/- 0.008)
Source: Frei & Gunn 1994, AJ, 108, 1476 (their Table 2).
- Conversion from STMAG magnitudes to Johnson magnitudes:
- See the WFPC2 Photometry Cookbook
- For more filters, see
Paul
Martini's useful data.
Photon Flux:
Given the passband and the magnitude of an object, the number of
tphotons incident at the top of the atmosphere may be estimated using
the data in this table:
| Band
| lambda_c
| dlambda/lambda
| Flux at m=0
| Reference
|
|
| um
|
| Jy
|
|
| U
| 0.36
| 0.15
| 1810
| Bessel (1979)
|
| B
| 0.44
| 0.22
| 4260
| Bessel (1979)
|
| V
| 0.55
| 0.16
| 3640
| Bessel (1979)
|
| R
| 0.64
| 0.23
| 3080
| Bessel (1979)
|
| I
| 0.79
| 0.19
| 2550
| Bessel (1979)
|
| J
| 1.26
| 0.16
| 1600
| Campins, Reike, & Lebovsky (1985)
|
| H
| 1.60
| 0.23
| 1080
| Campins, Reike, & Lebovsky (1985)
|
| K
| 2.22
| 0.23
| 670
| Campins, Reike, & Lebovsky (1985)
|
| g
| 0.52
| 0.14
| 3730
| Schneider, Gunn, & Hoessel (1983)
|
| r
| 0.67
| 0.14
| 4490
| Schneider, Gunn, & Hoessel (1983)
|
| i
| 0.79
| 0.16
| 4760
| Schneider, Gunn, & Hoessel (1983)
|
| z
| 0.91
| 0.13
| 4810
| Schneider, Gunn, & Hoessel (1983)
|
Also useful are these identities:
1 Jy = 10^-23 erg sec^-1 cm^-2 Hz^-1
1 Jy = 1.51e7 photons sec^-1 m^-2 (dlambda/lambda)
See also Strolger's
units page.
Example: How many V-band photons are incident per second on an area of
1 m^2 at the top of the atmosphere from a V=23.90 star?
From the table, the flux at V=0 is 3640 Jy; hence, at V=23.90 the flux
is diminished by a factor 10^(-0.4*V)=2.75e-10, yielding a flux of
1.e-6 Jy. Since dlambda/lambda=0.16 in V, the flux per second on a 1
m^2 aperture is
f=1.e-6 Jy * 1.51e7 * 0.16 = 2.42 photons sec^-1
Filter Transformations:
All filter transformations depend to some extent on the spectral type
of the object in question. If this is known, then you are probably
best off using the SYNPHOT package
in IRAF/STSDAS to compute the transformation. Some transformations
are listed below for convenience:
| Bands
| Equation
| Reference
|
| Gunn g to Johnson B:
| B = g + 0.51 + 0.60*(g-r)
| [1]
|
| Gunn g to Johnson V:
| V = g - 0.03 - 0.42*(g-r)
| [1]
|
| Gunn r to Mould R:
| R = r - 0.51 - 0.15*(g-r)
| [1]
|
| Gunn g to Photographic J:
| J = g + 0.39 + 0.37*(g-r)
| [1]
|
| Gunn r to Photographic F:
| F = r - 0.25 + 0.17*(g-r)
| [1]
|
| Gunn i to Mould I:
| I = i - 0.75 (approx)
| [1]
|
References:
- Windhorst, R. W., et al. 1991, ApJ, 380, 362
More recent calibrations can be found at the
SDSS website.
In particular,
Jester et al (2005)
give
| Color | Equation | | Color | Equation |
| u-g | 1.28*(U-B) + 1.13 | | U-B | 0.78*(u-g) - 0.88 |
| g-r | 1.02*(B-V) - 0.22 | | B-V | 0.98*(g-r) + 0.22 |
| r-i | 0.91*(Rc-Ic) - 0.20 | | V-R | 1.09*(r-i) + 0.22 |
| r-z | 1.72*(Rc-Ic) - 0.41 | | Rc-Ic | 1.00*(r-i) + 0.21 |
| g | V+0.60*(B-V) - 0.12 | | B | g+0.39*(g-r)+0.21 |
| r | V-0.42*(B-V) + 0.11 | | V | g-0.59*(g-r)-0.01 |
These appear to be convert between Gunn AB magnitudes and Johnson Vega magnitudes.
Night Sky Brightnesses:
These values are appropriate for taken from CTIO but should serve as
reasonable approximations for most dark sites:
| Lunar Age
| U
| B
| V
| R
| I
|
| (days)
|
| 0
| 22.0
| 22.7
| 21.8
| 20.9
| 19.9
|
| 3
| 21.5
| 22.4
| 21.7
| 20.8
| 19.9
|
| 7
| 19.9
| 21.6
| 21.4
| 20.6
| 19.7
|
| 10
| 18.5
| 20.7
| 20.7
| 20.3
| 19.5
|
| 14
| 17.0
| 19.5
| 20.0
| 19.9
| 19.2
|
Source: NOAO Newsletter #10.
Notice:
This material was adapted for the web from the appendix to the unpublished
manuscript Observations of Distant Galaxies by R. Kron and H.
Spinrad, without permission of the authors, by G. Wirth. This page
was copied without permission by S. McGaugh in 2001, who over the years has made
various practical additions (e.g., the solar absolute magnitude in various
bands; references to Landolt standards) until the source was unrecognizable.
There is probably some deep
lesson in this about how [mis]information propogates on the web, but
we're all too lazy to contemplate it.
This page in Romanian
This page in Indonesian
This page in German
