
There is a tendency when teaching science to oversimplify its history for the sake of getting on with the science. How it came to be isn't necessary to learn it. But to do science requires a proper understanding of the process by which it came to be.
The story taught to cosmology students seems to have become: we didn't believe in the cosmological constant (Λ), then in 1998 the Type Ia supernovae (SN) monitoring campaigns detected accelerated expansion, then all of a sudden we did believe in Λ. The actual history was, of course, rather more involved - to the point where this oversimplification verges on disingenuous. There were many observational indications of Λ that were essential in paving the way.
Modern cosmology starts in the early 20th century with the recognition that the universe should be expanding or contracting - a theoretical inevitability of General Relativity that Einstein initially tried to dodge by inventing the cosmological constant - and is expanding in fact, as observationally established by Hubble and Slipher and many others since. The Big Bang was largely considered settled truth after the discovery of the existence of the cosmic microwave background (CMB) in 1964.
The CMB held a puzzle, as it quickly was shown to be too smooth. The early universe was both isotropic and homogeneous. Too homogeneous. We couldn't detect the density variations that could grow into galaxies and other immense structures. Though such density variations are now well measured as temperature fluctuations that are statistically well described by the acoustic power spectrum, the starting point was that these fluctuations were a disappointing no-show. We should have been able to see them much sooner, unless something really weird was going on...
That something weird was non-baryonic cold dark matter (CDM). For structure to grow, it needed the helping hand of the gravity of some unseen substance. Normal matter matter did not suffice. The most elegant cosmology, the Einstein-de Sitter universe, had a mass density Ωm = 1. But the measured abundances of the light elements were only consistent with the calculations of big bang nucleosynthesis if normal matter amounted to only 5% of Ωm = 1. This, plus the need to grow structure, led to the weird but seemingly unavoidable inference that the universe must be full of invisible dark matter. This dark matter needed to be some slow moving, massive particle that does not interact with light nor reside within the menagerie of particles present in the Standard Model of Particle Physics.
CDM and early universe Inflation were established in the 1980s. Inflation gave a mechanism that drove the mass density to exactly one (elegant!), and CDM gave us hope for enough mass to get to that value. Together, they gave us the Standard CDM (SCDM) paradigm with Ωm = 1.000 and H0 = 50 km/s/Mpc.
 |
| I was there when SCDM failed. |
It is hard to overstate the ferver with which the SCDM paradigm was believed. Inflation required that the mass density be exactly one; Ωm < 1 was inconceivable. For an Einstein-de Sitter universe to be old enough to contain the oldest stars, the Hubble constant had to be the lower of the two (50 or 100) commonly discussed at that time. That meant that H0 > 50 was Right Out. We didn't even discuss Λ. Λ was Unmentionable. Unclean.
SCDM was Known, Khaleesi.
 |
Λ had attained unmentionable status in part because of its origin as Einstein's greatest blunder, and in part through its association with the debunked Steady State model. But serious mention of it creeps back into the literature by 1990. The first time I personally heard Λ mentioned as a serious scientific possibility was by Yoshii at a conference in 1993. Yoshii based his argument on a classic cosmological test, N(m) - the number of galaxies as a function of how faint they appeared. The deeper you look, the more you see, in a way that depends on the intrinsic luminosity of galaxies, and how they fill space. Look deep enough, and you begin to trace the geometry of the cosmos.
At this time, one of the serious problems confronting the field was the faint blue galaxies problem. There were so many faint galaxies on the sky, it was incredibly difficult to explain them all. Yoshii made a simple argument. To get so many galaxies, we needed a big volume. The only way to do that in the context of the Robertson-Walker metric that describes the geometry of the universe is if we have a large cosmological constant, Λ. He was arguing for ΛCDM five years before the SN results.
 |
| Lambda? We don't need no stinking Lambda! |
Yoshii was shouted down. NO! Galaxies evolve! We don't need no stinking Λ! In retrospect, Yoshii & Peterson (1995) looks like a good detection of Λ. Perhaps Yoshii & Peterson also deserve a Nobel prize?
Indeed, there were many hints that Λ (or at least low Ωm) was needed, e.g., the baryon catastrophe in clusters, the power spectrum of IRAS galaxies, the early appearance of bound structures, the statistics of gravitational lenses, and so on. Certainly by the mid-90s it was clear that we were not going to make it to Ωm = 1. Inflation was threatened - it requires Ωm = 1 - or at least a flat geometry: Ωm+ΩΛ = 1.
SCDM was in crisis.
A very influential 1995 paper by Ostriker & Steinhardt did a lot to launch ΛCDM. I was impressed by the breadth of data Ostriker & Steinhardt discussed, all of which demanded low Ωm. I thought the case for Λ was less compelling, as it hinged on the age problem in a way that might also have been solved, at that time, by simply having an open universe (low Ωm with no Λ). This would ruin Inflation, but I wasn't bothered by that. I expect they were. Regardless, they definitely made that case for ΛCDM three years before the supernovae results. Their arguments were accepted by almost everyone who was paying attention, including myself. I heard Ostriker give a talk around this time during which he was asked "what cosmology are you assuming?" to which he replied "the right one." Called the "concordance" cosmology by Ostriker & Steinhardt, ΛCDM had already achieved the status of most-favored cosmology by the mid-90s.
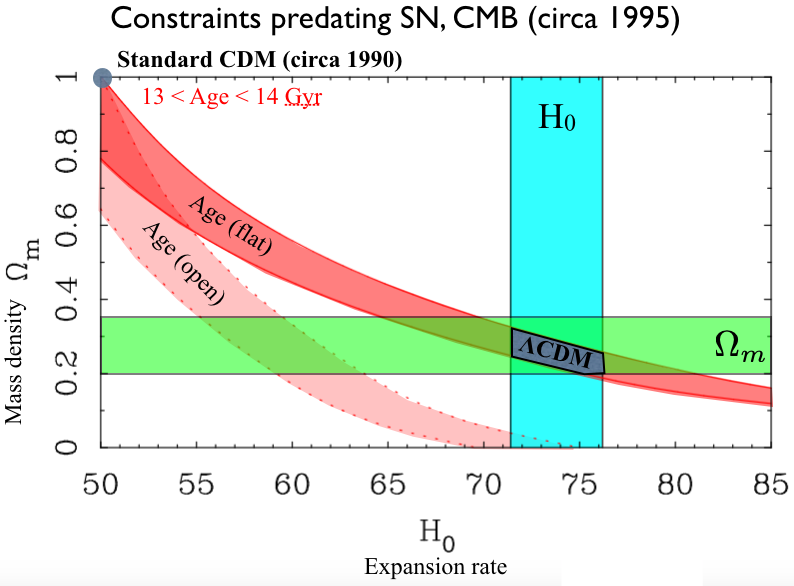 |
| A simplified version of the diagram of Ostriker & Steinhardt (1995) illustrating just a few of the constraints they discussed. Direct measurements of the expansion rate, mass density, and ages of the oldest stars excluded SCDM, instead converging on a narrow window - what we now call ΛCDM. |
Ostriker & Steinhardt neglected to mention an important prediction of Λ: not only should the universe expand, but that expansion rate should accelerate! In 1995, that sounded completely absurd. People had looked for such an effect, and claimed not to see it. So I wrote a brief note pointing out the predicted acceleration of the expansion rate. I meant it in a bad way: how crazy would it be if the expansion of the universe was accelerating?! This was an obvious and inevitable consequence of ΛCDM that was largely being swept under the rug at that time.
I mean[t], surely we could live with Ωm < 1 but no Λ. Can't we all just get along? Not really, as it turned out. I remember Mike Turner pushing the SN people very hard in Aspen in 1997 to Admit Λ. He had an obvious bias: as an Inflationary cosmologist, he had spent the previous decade castigating observers for repeatedly finding Ωm < 1. That's too little mass, you fools! Inflation demands Ωm = 1.000! Look harder!
By 1997, Turner had, like many cosmologists, finally wrapped his head around the fact that we weren't going to find enough mass for Ωm = 1. This was a huge problem for Inflation. The only possible solution, albeit an ugly one, was if Λ made up the difference. So there he was at Aspen, pressuring the people who observed supernova to Admit Λ. One, in particular, was Richard Ellis, a great and accomplished astronomer who had led the charge in shouting down Yoshii. They didn't yet have enough data to Admit Λ. Not.Yet.
By 1998, there were many more high redshift SNIa. Enough to see Λ. This time, after the long series of results only partially described above, we were intellectually prepared to accept it - unlike in 1993. Had the SN experiments been conducted five years earlier, and obtained exactly the same result, they would not have been awarded the Nobel prize. They would instead have been dismissed as a trick of astrophysics: the universe evolves, metallicity was lower at earlier times, that made SN then different from now, they evolve and so cannot be used as standard candles. This sounds silly now, as we've figured out how to calibrate for intrinsic variations in the luminosities of Type Ia SN, but that is absolutely how we would have reacted in 1993, and no amount of improvements in the method would have convinced us. This is exactly what we did with faint galaxy counts: galaxies evolve; you can't hope to understand that well enough to constrain cosmology. Do you ever hear them cited as evidence for Λ?
Great as the supernovae experiments to measure the metric genuinely were, they were not a discovery so much as a confirmation of what cosmologists had already decided to believe. There was no singular discovery that changed the way we all thought. There was a steady drip, drip, drip of results pointing towards Λ all through the '90s - the age problem in which the oldest stars appeared to be older than the universe in which they reside, the early appearance of massive clusters and galaxies, the power spectrum of galaxies from redshift surveys that preceded Sloan, the statistics of gravitational lenses, and the repeated measurement of 1/4 < Ωm < 1/3 in a large variety of independent ways - just to name a few. By the mid-90's, SCDM was dead. We just refused to bury it until we could accept ΛCDM as a replacement. That was what the Type Ia SN results really provided: a fresh and dramatic reason to accept the accelerated expansion that we'd already come to terms with privately but had kept hidden in the closet.
Note that the acoustic power spectrum of temperature fluctuations in the cosmic microwave background (as opposed to the mere existence of the highly uniform CMB) plays no role in this history. That's because temperature fluctuations hadn't yet been measured beyond their rudimentary detection by COBE. COBE demonstrated that temperature fluctuations did indeed exist (finally!) as they must, but precious little beyond that. Eventually, after the settling of much dust, COBE was recognized as one of many reasons why Ωm ≠ 1, but it was neither the most clear nor most convincing reason at that time. Now, in the 21st century, the acoustic power spectrum provides a great way to constrain what all the parameters of ΛCDM have to be, but it was a bit player in its development. The water there was carried by traditional observational cosmology using general purpose optical telescopes in a great variety of different ways, combined with a deep astrophysical understanding of how stars, galaxies, quasars and the whole menagerie of objects found in the sky work. All the vast knowledge incorporated in textbooks like those by Harrison, by Peebles, and by Peacock - knowledge that often seems to be lacking in scientists trained in the post-WMAP era.
Despite being a late arrival, the CMB power spectrum measured in 2000 by Boomerang and 2003 by WMAP did one important new thing to corroborate the ΛCDM picture. The supernovae data didn't detect accelerated expansion so much as exclude the deceleration we had nominally expected. The data were also roughly consistent with a coasting universe (neither accelerating nor decelerating); the case for acceleration only became clear when we assumed that the geometry of the universe was flat (Ωm+ΩΛ = 1). That didn't have to work out, so it was a great success of the paradigm when the location of the first peak of the power spectrum appeared in exactly the right place for a flat FLRW geometry.
The consistency of these data have given ΛCDM an air of invincibility among cosmologists. But a modern reconstruction of the Ostriker & Steinhardt diagram leaves zero room remaining - hence the tension between H0 = 73 measured directly and H0 = 67 from multiparameter CMB fits.
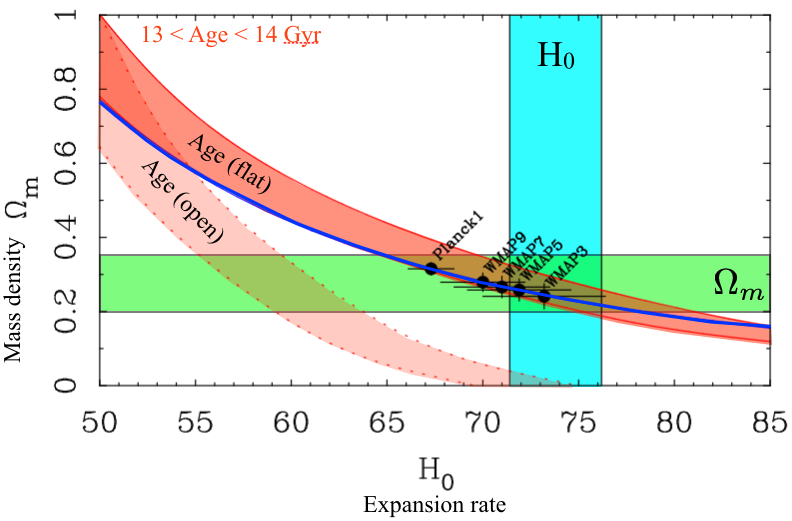 |
| Constraints from the acoustic power spectrum of the CMB overplotted on the direct measurements from the plot above. Initially in great consistency with those measurement, the best fit CMB values have steadily wandered away from the most-favored region of parameter space that established ΛCDM in the first place. This is most apparent in the tension with H0. |
In cosmology, we are accustomed to having to find our way through apparently conflicting data. The difference between an expansion rate of 67 and 73 seems trivial given that the field was long riven - in living memory - by the dispute between 50 and 100. This gives rise to the expectation that the current difference is just a matter of some subtle systematic error somewhere. That may well be correct. But it is also conceivable that FLRW is inadequate to describe the universe, and we have been driven to the objectively bizarre parameters of ΛCDM because it happens to be the best approximation that can be obtained to what is really going on when we insist on approximating it with FLRW.
Though a logical possibility, that last sentence will likely drive many cosmologists to reach for their torches and pitchforks. Before killing the messenger, we should remember that we once endowed SCDM with the same absolute certainty we now attribute to ΛCDM. I was there, 3,000 internet years ago, when SCDM failed. There is nothing so sacred in ΛCDM that it can't suffer the same fate, as has every single cosmology ever devised by humanity.
Today, we still lack definitive knowledge of either dark matter or dark energy. These add up to 95% of the mass-energy of the universe according to ΛCDM. These dark materials must exist.
It is Known, Khaleesi.