Within the uncertainties, both theoretical and experimental, the peak amplitude ratio is bang on what I predicted it would be (McGaugh 1999) for the case of no CDM. When BOOMERanG first reported observations of the first and second peaks, the smallness of the second peak came as a great surprise. No CDM was the only model to correctly predict this in advance. Moreover, the follow-on prediction that precisely this ratio would be observed when the second peak became well resolved has now been realized.

What about the third peak?
This remains the billion Eruo question (or however much it will cost to fly the Planck mission). Page et al. (2003) do not offer a WMAP measurement of the third peak. They do quote a compilation of other experiments by Wang et al. (2003). Taking this number at face value, the second to third peak amplitude ratio is A_2:3 = 1.03 +/- 0.20. The LCDM expectation value for this quantity was 1.1, while the No-CDM expectation was 1.9. By this measure, LCDM is clearly preferable, in contradiction to the better measured first-to-second peak ratio.

It is far from obvious that we can trust the measurements of the third peak yet. Various experiments give various answers, and the uncertainty emerging from any compilation depends on the accuracy of the calibrations of the experiments which contribute to it. Anyone who has tried to measure things on the sky knows how hard this is to do. And those who haven't had this experience only need look at the calibration correction made by the BOOMERanG experiment between their 2000 and 2001 data release. Simply looking at the various data around L ~ 800, it does look like there could well be systematic calibration discrepancies between different experiments. This is why, for a proper test, you want all three peaks to be measured accurately by the same experiment. This has not happened.

LCDM fits the WMAP data very well. Why do the 1:2 and 2:3 peak ratios give different answers?

WMAP power spectrum with LCDM fit

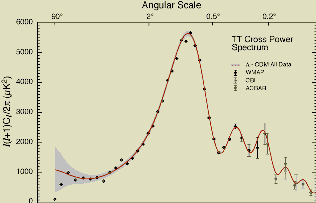LCDM has many free parameters. The existence test I had proposed for CDM only works in CMB data if we have foreknowledge (a "strong proir") of the baryon density. For a long time, Big Bang Nucleosynthesis, combined with the measured abundances of the light elements (deuterium, helium, and lithium), implied that O_bh²=0.0125. In 1999 when I made the prediction, I considered the full range of baryon densities consistent with this. By 2000, opinion seemed to be that the best value for the baryon density was O_bh²=0.019 (Tytler et al. 2000), at the high end of the former range. Then the initial BOOMERanG results showed a small (if any) second peak, and CDM models started driving up the baryon density to satisfy this: for a whole year, many people thought O_bh² > 0.03. Oddly enough, once this happened, some deuterium measurements in high redshift QSOs began to imply high baryon densities. These measurements are not mutually consistent and are too high for the helium and lithium constraints. Until we agree on a firm value for the baryon density which is independent of CMB measurements, then there is no test.

In LCDM models, the amplitude of the second peak is suppressed relative to the first by increasing the baryon density. So, in addition to predicting the correct amplitude ratio, I further predicted that LCDM fits would find high baryon densities. This has come to pass, with O_bh²=0.024 fequently being quoted. That is a lot of baryons, and a long way from the best value for the best determined quantity in cosmology as of only a few years ago. The CMB measurements are still not competetive with abundance measurements for constraining the baryon density, as there is a further degeneracy in the "tilt" (n) of the power spectrum. Some fits are now finding n < 1, which also has the effect of reducing the second peak amplitude. The best fit WMAP model (Spergel et al. 2003) does a bit of both: O_bh²=0.022 and n = 0.93. So long as we're willing to play this game, there is no test for the existence of CDM in the CMB data. A negative test only occurs if CMB and BBN results clearly conflict, or if the CMB data themselves can not be fit with a CDM component. Marginal agreement (the situation currently) certainly does not falsify CDM, but neither does it confirm it.

That said, it is not obvious to me that a simple No-CDM model can match the absolute amplitudes of the peaks. It may well be that the WMAP are now good enough to demand a proper treatment with a relativistic version of MOND. If so, these data provide strong empirical constraints on the form any such theory must take. The lack of such a theory is certainly unfortunate, but in its absence the CMB data can neither confirm nor falsify MOND.

It does appear that whatever the underlying [MOND?] cosmology is, it has to share many properties of LCDM. A Friedmann model with the correct LCDM parameters would appear to be the correct effective cosmology. It would seem rather unlikely that this would just fall out of the "right" relativistic MOND cosmology. By the same coin, if LCDM is really right, it must explain the observed MOND phenomena in indidual galaxies. Though few people seem to appreciate it, this is extraordinarilly difficult to do. Hence, both alternatives seem impossibly difficult.

There remain some substantial puzzles for cosmology as well. Not all is well for LCDM in the CMB data. The model which best fits the C_L power spectrum fails to fit the real space power spectrum C(theta) at high significance (>99% c.l.) (Spergel et al. 2003). The data have power consistent with zero on scales >60 degrees, a very peculiar result in the context of any inflationary model. (This same result had previously been obtained by COBE.)

To me, the greater question is whether the paradigm is right. There have been plenty of occassions on which humans have been quite sure the had the right cosmological model. Though we don't burn people at the stake any more, I am not so sure we are all that much smarter than our forebearers who made this mistake of hubris. I would be more comfortable if the best fit LCDM parameters made any sense, but they do not (having been called "preposterous" by even the most vocal advocates). Yes, a Friedmann model fits the cosmic scale data, but we have had to invoke two tooth fairies in order to accomplish this: dark matter and dark energy. The existence of both these components remains supposition based on the presumption of the correctness of the underlying model. Perhaps the silliness of the parameters we find is an indication that something is broken. Certainly, we have no business claiming that cosmology is a solved problem at least until we confirm the existence of non-baryonic dark matter by laboratory experiments. The LCDM model which works so well to describe the CMB data only does so if this stuff really exists, and in the correct amount.

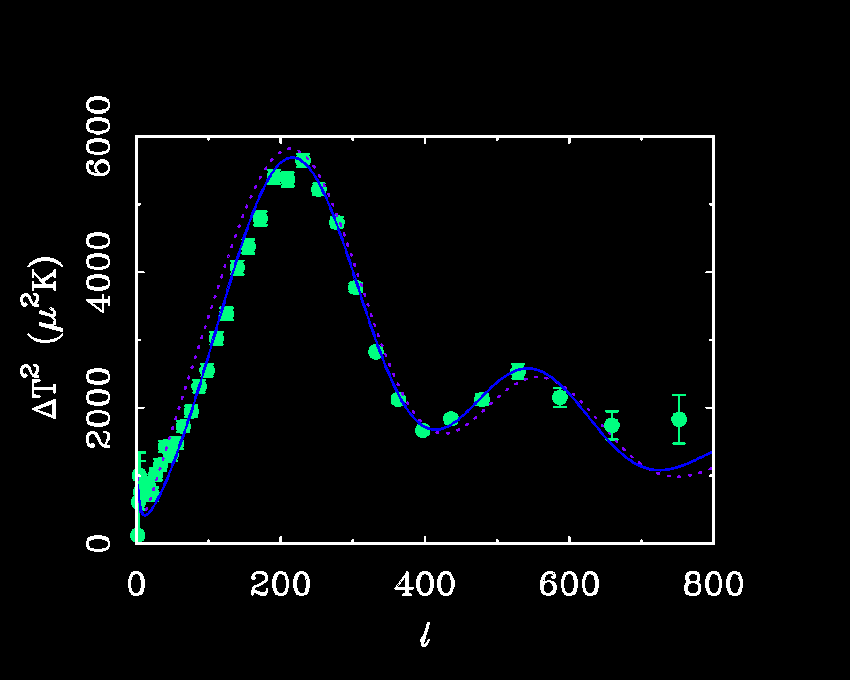The binned WMAP data obtained from LAMBDA. Overplotted as the dotted purple line is the no-CDM model (unretouched since the fit to the BOOMERanG data). This does a reasonable job of matching the peak amplitudes. The biggest discrepancy appears to be in the width of the peaks and their precise positions. The latter is very sensitive to geometry; the former may indicate a significant neutrino mass. Plotted in blue is an old (1999) model I found lurking about on disk with a mean neutrino mass of ~2/3 eV, with geometry and normalization tweaked by eye to fit. This seems pretty good for such a crude analysis.

Finally, cosmological data are approaching the accuracy of rotation curves.

© Stacy McGaugh, February 17, 2003; last edited February 21, 2003

Return to the MOND pages home page

Well, which is it?