Predicting dwarf galaxy velocity dispersions
Suppose the Milky Way is discovered to have a new dwarf satellite galaxy with the following properties:
| D = 200 kpc | Re = 1 kpc | M* = 105 M☉ |
-
Method 1: Newton
- Use the virial relation to predict the velocity dispersion assuming that
the only mass present is that of the stars.
Method 2: Abundance Matching:
Fig. 6 of the review by Bullock & Boylan-Kolchin (arXiv:1707.04256) shows the relation between stellar mass and halo mass (and Vmax of the halo) obtained from abundance matching. Use this graph to - Estimate the halo mass and the range of plausible halo masses.
- Estimate the corresponding velocity dispersion and its range.
[You may assume σ = Vmax/√3] - For this velocity, compute the dynamical mass and the ratio of dynamical to stellar mass.
- Is this mass consistent with the halo mass? If not, why not?
Method 3: MOND
The velocity dispersion estimator for an isolated object in the deep MOND regime is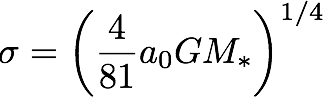
[You can find the value of a0 on the useful numbers page.]
- What is the velocity dispersion predicted by MOND for this system, assuming it is isolated?
- Check that this dwarf is in the MOND regime.
[This formula applies only for very low accelerations, when the internal acceleration gin = 3 σ2/r1/2 is less than a0.]
[The 3D half-light radius r1/2 is commonly assumed to be (4/3) times the measured projected (2D) effective radius: r1/2 = (4/3) Re.]Distinguishing the predictions:
The best observational accuracy that is typically obtained for the velocity dispersion in such systems is ± 2 km/s. - Should it be possible to distinguish between the hypotheses above?
ASTR 433 only:
Method 4: the External Field Effect
A unique feature of MOND is the external field effect (EFE). When the external field gex of the host exceeds the internal field of the dwarf satellite, the velocity dispersion estimator becomes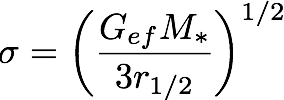
where Gef ≈ (a0/gex)G. This quasi-Newtonian regime has a higher effective value for Newton's constant.
- Is this dwarf in the isolated or quasi-Newtonian regime?
I.e., is gin > gex or gin < gex?
[To estimate gex, assume the rotation curve of the Milky Way remains flat at 200 km/s.]- What is the velocity dispersion predicted for this system considering the EFE?
- Can this be distinguished from the isolated case?
- Is this dwarf in the isolated or quasi-Newtonian regime?
Brown dwarf MACHOs
- Early on, brown dwarfs were a popular dark matter candidate.
Presuming that the typical brown dwarf has a mass of 0.02 M☉,
and recalling the result for the local density of dark matter from the
first homework (0.015 M☉pc-3),
what local number density would be required for brown
dwarfs to be the dark matter in the Milky Way? What is the corresponding separation
between these brown dwarfs?
- The optical depth τ of gravitational lensing for MACHOs in the halo is
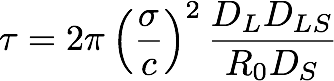
- What is the optical depth τ to gravitational lensing from a halo of brown dwarfs
in the direction of the LMC?
Hint: We are 8 kpc from the Galactic Center; the LMC is 50 kpc away. Where is the typical lens? What is its typical speed (σ)? - The observed limit found by EROS
is τ < 3.6 x 10-8. How does this compare with the optical depth you computed?
What does this imply?
- The EROS limit only applies for objects of mass > 10-8 M☉.
What famous solar system object has about this mass? What local number density and
typical separation would such objects have if they were to be the dark matter?
Would we notice them?
ASTR 433 only:
What would the kinetic energy of such a halo object should it happen to collide with the Earth? How does this compare with the gravitational binding energy of the Earth?
WIMPs in you
- Assuming the dark matter is made of WIMP mass of 100 GeV, how many are passing through your body at any given moment?
Cosmic Microwave Background Radiation
The microwave background consists of relict radiation in a blackbody distribution withTCMB = 2.7 K and energy density jCMB = 4 x 10-13 ergs cm-3.
- What is the number density of photons?
- If the mean mass density of baryons in the universe is
ρ0 = 2 x 10-31 g cm-3, what is the number
density of baryons?
- What is the baryon-to-photon ratio?
Ωm from Cluster Baryon Fractions
Use the data in the table (from White & Fabian 1995) to compute the baryon fractions of these clusters (you may neglect stars, presuming the gas mass is most of the baryons). If Big Bang Nucleosynthesis tells us the baryon density Ωb h2 = 0.02, what is Ωm?How does your answer depend on the Hubble constant?
Is the scatter in fb consistent with the quoted errors?
[It may help to make a plot of some relevant quantities.]
| Cluster | Mgas | ErrMgas | Mtot |
| Coma | 5.1 | 1.5 | 17 |
| A85 | 0.87 | 0.06 | 4.64 |
| A401 | 1.32 | 0.07 | 10.1 |
| A478 | 2.38 | 0.21 | 9.28 |
| A545 | 1.91 | 0.25 | 10.6 |
| A644 | 0.95 | 0.06 | 9.06 |
| A665 | 4.37 | 0.46 | 22.1 |
| A1413 | 1.83 | 0.23 | 15.9 |
| A1650 | 0.75 | 0.08 | 6.37 |
| A1689 | 2.12 | 0.16 | 15.5 |
| A1763 | 2.61 | 0.22 | 13.2 |
| A1795 | 1.13 | 0.08 | 5.49 |
| A2009 | 1.44 | 0.10 | 10.6 |
| A2029 | 1.26 | 0.11 | 10.3 |
| A2142 | 2.84 | 0.15 | 20.1 |
| A2163 | 5.46 | 0.49 | 32.5 |
| A2319 | 1.73 | 0.12 | 14.2 |
| A3186 | 1.76 | 0.23 | 9.50 |
| A3266 | 1.42 | 0.07 | 9.07 |
| A3888 | 1.20 | 0.15 | 8.66 |
These data assume H0 = 50 km s-1 Mpc-1.
Mgas and Mtot are in units of 1014 Mo.
Mgas scales as h^-5/2 (roughly),
Mtot as h^-1.